Büchi's Problem
Encyclopedia
Büchi's problem, also known as the n squares' problem, is an open problem from number theory
named after the Swiss mathematician Julius Richard Büchi
. It asks whether there is a positive integer M such that any sequence of M or more integer squares, whose second difference is constant and equal to 2, is necessarily a sequence of squares of the form (x + i)2, i = 1, 2, ..., M,... for some integer x. In 1983, Douglas Hensley observed that Büchi's problem is equivalent to the following: Does there exist a positive integer M such that, for all integers x and a, the quantity (x + n)2 + a cannot be a square for more than M consecutive values of n, unless a = 0?
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
named after the Swiss mathematician Julius Richard Büchi
Julius Richard Büchi
Julius Richard Büchi was a Swiss logician and mathematician.He received his Dr. sc. nat. in 1950 at the ETH Zürich under supervision of Paul Bernays and Ferdinand Gonseth. Shortly afterwards he went to Purdue University, Lafayette, Indiana...
. It asks whether there is a positive integer M such that any sequence of M or more integer squares, whose second difference is constant and equal to 2, is necessarily a sequence of squares of the form (x + i)2, i = 1, 2, ..., M,... for some integer x. In 1983, Douglas Hensley observed that Büchi's problem is equivalent to the following: Does there exist a positive integer M such that, for all integers x and a, the quantity (x + n)2 + a cannot be a square for more than M consecutive values of n, unless a = 0?
Statement of Büchi's problem
Büchi's problem can be stated in the following way: Does there exist a positive integer M such that the system of equations-
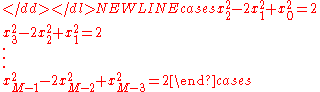
has only solutions satisfying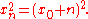
Since the first difference of the sequence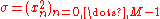
is the sequence 
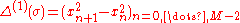, the second difference of 
is
-
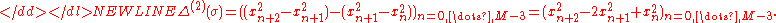
Therefore, the above system of equations is equivalent to the single equation
where the unknown is the sequence
.
Examples
Observe that for any integer x we have
Hence the equation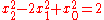
has solutions, called trivial Büchi sequences of length three, such that 
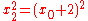and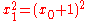 
. For example, the sequences (2, 3, 4) and (2, −3, 4) are trivial Büchi sequences. A nontrivial Büchi sequence of length three is given for example by the sequence (0, 7, 10), as it satisfies 102 − 2·72 + 02 = 2, while 02, 72 and 102 are not consecutive squares.
Replacing x by x + 1 in equation
, we obtain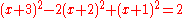 
. Hence the system of equations
-
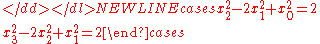
has trivial Büchi solutions of length 4, namely the one satisfying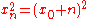
for n = 0, 1, 2, 3. In 1983, D. Hensley showed that there are infinitely many nontrivial Büchi sequences of length four. It is not known whether there exist any non-trivial Büchi sequence of length five (Indeed, Büchi asked originally the question only for M = 5.).
Original motivation
A positive answer to Büchi's Problem would imply, using the negative answer to Hilbert's Tenth ProblemHilbert's tenth problemHilbert's tenth problem is the tenth on the list of Hilbert's problems of 1900. Its statement is as follows:Given a Diophantine equation with any number of unknown quantities and with rational integral numerical coefficients: To devise a process according to which it can be determined in a finite...
by Yuri MatiyasevichYuri MatiyasevichYuri Vladimirovich Matiyasevich, is a Russian mathematician and computer scientist. He is best known for his negative solution of Hilbert's tenth problem, presented in his doctoral thesis, at LOMI .- Biography :* In 1962-1963 studied at Saint Petersburg Lyceum 239...
, that there is no algorithm to decideDecidability (logic)In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
whether a system of diagonal quadratic forms with integer coefficients represents an integer tuple. Indeed, Büchi observed that squaring, therefore multiplication, would be existentially definable in the integers over the first-orderFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
language having two symbols of constant for 0 and 1, a symbol of function for the sum, and a symbol of relation P to express that an integer is a square.
Some results
Paul VojtaPaul VojtaPaul Alan Vojta is an American mathematician, known for his work in number theory on diophantine geometry and diophantine approximation....
proved in 1999 that a positive answer to Büchi's Problem would follow from a positive answer to a weak version of the Bombieri-Lang conjecture. In the same article, he proves that the analogue of Büchi's Problem for the field of meromorphic functions over the complex numbers has a positive answer. Positive answers to analogues of Büchi's Problem in various other rings of functions have been obtained since then (in the case of rings of functions, one adds the hypothesis that not all xn are constant).
-
-
