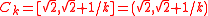Cantor's intersection theorem
Encyclopedia
In real analysis
, a branch of mathematics, Cantor's intersection theorem, named after Georg Cantor
, is a theorem related to compact sets in R, the set of real number
s. It states that a decreasing nested sequence
of non-empty, closed
and bounded
subsets of R has nonempty intersection. In other words, supposing {Ck} is a sequence of non-empty, closed and bounded sets satisfying

it follows that

The result is typically used as a lemma in proving the Heine–Borel theorem, which states that sets of real numbers are compact if and only if they are closed and bounded. Conversely, if the Heine–Borel theorem is known, then it can be restated as: a decreasing nested sequence of non-empty, compact subsets of R has nonempty intersection.
As an example, if Ck = [0, 1/k], the intersection over {Ck} is {0}. On the other hand, both the sequence of open bounded sets Ck = (0, 1/k) and the sequence of unbounded closed sets Ck = [k, ∞) have empty intersection. All these sequences are properly nested.
The theorem generalizes to Rn, the set of n-element vectors of real numbers, but does not generalize to arbitrary metric space
s. For example, in the space of rational number
s, the sets
are closed and bounded, but their intersection is empty.
A simple corollary of the theorem is that the Cantor set
is nonempty, since it is defined as the intersection of a decreasing nested sequence of sets, each of which is defined as the union of a finite number of closed intervals; hence each of these sets is non-empty, closed, and bounded. In fact, the Cantor set contains uncountably many points.
over the non-empty Ck. Because Ck is closed, ak belongs to Ck; because the sets are decreasing nested, the sequence is monotonic increasing. Because it is also bounded (being contained in the bounded set C1), it must converge to some limit L. Choose any j ≥ 1; the subsequence of (ak) for k ≥ j is contained in Cj and converges to L. Since Cj is closed, L lies in Cj. Since this is true for all j, L lies in all Cj, and so in their intersection.
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, a branch of mathematics, Cantor's intersection theorem, named after Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
, is a theorem related to compact sets in R, the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. It states that a decreasing nested sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of non-empty, closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
subsets of R has nonempty intersection. In other words, supposing {Ck} is a sequence of non-empty, closed and bounded sets satisfying

it follows that

The result is typically used as a lemma in proving the Heine–Borel theorem, which states that sets of real numbers are compact if and only if they are closed and bounded. Conversely, if the Heine–Borel theorem is known, then it can be restated as: a decreasing nested sequence of non-empty, compact subsets of R has nonempty intersection.
As an example, if Ck = [0, 1/k], the intersection over {Ck} is {0}. On the other hand, both the sequence of open bounded sets Ck = (0, 1/k) and the sequence of unbounded closed sets Ck = [k, ∞) have empty intersection. All these sequences are properly nested.
The theorem generalizes to Rn, the set of n-element vectors of real numbers, but does not generalize to arbitrary metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. For example, in the space of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, the sets
are closed and bounded, but their intersection is empty.
A simple corollary of the theorem is that the Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
is nonempty, since it is defined as the intersection of a decreasing nested sequence of sets, each of which is defined as the union of a finite number of closed intervals; hence each of these sets is non-empty, closed, and bounded. In fact, the Cantor set contains uncountably many points.
Proof
Consider the sequence (ak) where ak is the infimumInfimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
over the non-empty Ck. Because Ck is closed, ak belongs to Ck; because the sets are decreasing nested, the sequence is monotonic increasing. Because it is also bounded (being contained in the bounded set C1), it must converge to some limit L. Choose any j ≥ 1; the subsequence of (ak) for k ≥ j is contained in Cj and converges to L. Since Cj is closed, L lies in Cj. Since this is true for all j, L lies in all Cj, and so in their intersection.