See also Carathéodory's theorem

Carathéodory's theorem

In mathematics, Carathéodory's theorem may refer to one of a number of results of Constantin Carathéodory:*Carathéodory's theorem , about the extension of conformal mappings to the boundary...

 for other meanings

In convex geometry

Convex geometry

Convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space.Convex sets occur naturally in many areas of mathematics: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming,...

 Carathéodory's theorem states that if a point x of R

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

^d lies in the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

 of a set P, there is a subset P′ of P consisting of d+1 or fewer points such that x lies in the convex hull of P′. Equivalently, x lies in an r-simplex

Simplex

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

 with vertices in P, where . The result is named for Constantin Carathéodory

Constantin Carathéodory

Constantin Carathéodory was a Greek mathematician. He made significant contributions to the theory of functions of a real variable, the calculus of variations, and measure theory...

, who proved the theorem in 1911 for the case when P is compact. In 1914 Ernst Steinitz

Ernst Steinitz

Ernst Steinitz was a German mathematician.- Biography :Steinitz was born in Laurahütte , Silesia, Germany , the son of Sigismund Steinitz, a Jewish coal merchant, and his wife Auguste Cohen; he had two brothers. He studied at the University of Breslau and the University of Berlin, receiving his Ph.D...

 expanded Carathéodory's theorem for any sets P in R^d.

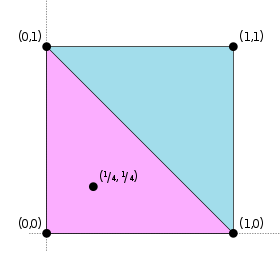
For example, consider a set P = {(0,0), (0,1), (1,0), (1,1)} which is a subset of R². The convex hull of this set is a square. Consider now a point x = (1/4, 1/4), which is in the convex hull of P. We can then construct a set {(0,0),(0,1),(1,0)} = P ′, the convex hull of which is a triangle and encloses x, and thus the theorem works for this instance, since |P′| = 3. It may help to visualise Carathéodory's theorem in 2 dimensions, as saying that we can construct a triangle consisting of points from P that encloses any point in P.

Proof

Let x be a point in the convex hull of P. Then, x is a convex combination

Convex combination

In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....

 of a finite number of points in P :


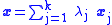
where every x_j is in P, every λ_j is positive, and .

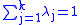Suppose k > d + 1 (otherwise, there is nothing to prove). Then, the points x₂ − x₁, ..., x_k − x₁ are linearly dependent

Linear independence

In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...

,

so there are real scalars μ₂, ..., μ_k, not all zero, such that


If μ₁ is defined as


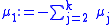
then


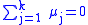
and not all of the μ_j are equal to zero. Therefore, at least one μ_j>0. Then,


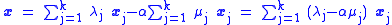
for any real α. In particular, the equality will hold if α is defined as


Note that α>0, and for every j between 1 and k,

In particular, λ_i − αμ_i = 0 by definition of α. Therefore,


where every is nonnegative, their sum is one , and furthermore, 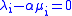. In other words, x is represented as a convex combination of at most k-1 points of P. This process can be repeated until x is represented as a convex combination of at most d + 1 points in P.

An alternative proof uses Helly's theorem

Helly's theorem

Helly's theorem is a basic result in discrete geometry describing the ways that convex sets may intersect each other. It was discovered by Eduard Helly in 1913, but not published by him until 1923, by which time alternative proofs by and had already appeared...

.

See also

• Shapley–Folkman lemma
  Shapley–Folkman lemma
  In geometry and economics, the Shapley–Folkman lemma describes the Minkowski addition of sets in a vector space. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integers zero and one to itself yields the set consisting of...
  
  
• Helly's theorem
  Helly's theorem
  Helly's theorem is a basic result in discrete geometry describing the ways that convex sets may intersect each other. It was discovered by Eduard Helly in 1913, but not published by him until 1923, by which time alternative proofs by and had already appeared...
  
  
• Krein–Milman theorem
• Choquet theory
  Choquet theory
  In mathematics, Choquet theory is an area of functional analysis and convex analysis created by Gustave Choquet. It is concerned with measures with support on the extreme points of a convex set C...
  
  

External links

• Concise statement of theorem in terms of convex hulls (at PlanetMath
  PlanetMath
  PlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
  
  )