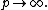Carleman's inequality
Encyclopedia
Carleman's inequality is an inequality in mathematics
, named after Torsten Carleman
, who proved it in 1923 and used it to prove Carleman's condition
for the determinancy of the problem of moments.
of non-negative real number
s, then
The constant e
in the inequality is optimal, that is, the inequality does not always hold if e is replaced by a smaller number. The inequality is strict (it holds with "<" instead of "≤") if all the elements in the sequence are positive.
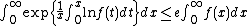
for any f ≥ 0.
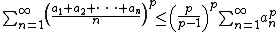
for the non-negative numbers
and 
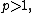replacing each 
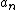with 
and letting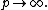 
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, named after Torsten Carleman
Torsten Carleman
Torsten Carleman , born Tage Gills Torsten Carleman, was a Swedish mathematician....
, who proved it in 1923 and used it to prove Carleman's condition
Carleman's condition
In mathematics, Carleman's condition is a sufficient condition for the determinacy of the moment problem.-Hamburger moment problem:For the Hamburger moment problem, the theorem, proved by Torsten Carleman, states the following:...
for the determinancy of the problem of moments.
Statement
Let a1, a2, a3, ... be a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of non-negative real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, then
The constant e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
in the inequality is optimal, that is, the inequality does not always hold if e is replaced by a smaller number. The inequality is strict (it holds with "<" instead of "≤") if all the elements in the sequence are positive.
Integral version
Carleman's inequality has an integral version, which states that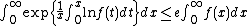for any f ≥ 0.
Proof
One can prove Carleman's inequality by starting with Hardy's inequality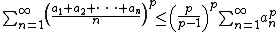for the non-negative numbers
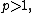and replacing each 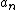with and letting