Casey's theorem
Encyclopedia
In mathematics
, Casey's theorem, also known as the generalized Ptolemy's theorem
, is a theorem in Euclidean geometry
named after the Irish mathematician
John Casey
.
 Let
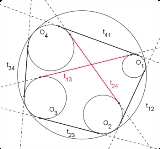
Let  be a circle of radius
be a circle of radius  . Let
. Let  be (in that order) four non-intersecting circles that lie inside
be (in that order) four non-intersecting circles that lie inside  and tangent to it. Denote by
and tangent to it. Denote by 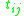 the length of the exterior common tangent of the circles
the length of the exterior common tangent of the circles 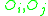 . Then:
. Then:

Note that in the degenerate case, where all four circles reduce to points, this is exactly Ptolemy's theorem
.
 by
by 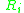 and its tangency point with the circle
and its tangency point with the circle  by
by 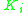 . We will use the notation
. We will use the notation 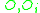 for the centers of the circles.
for the centers of the circles.
Note that from Pythagorean theorem
,
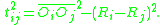
We will try to express this length in terms of the points . By the law of cosines
. By the law of cosines
in triangle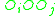 ,
,

Since the circles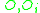 tangent to each other:
tangent to each other:

Let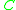 be a point on the circle
be a point on the circle  . According to the law of sines
. According to the law of sines
in triangle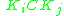 :
:
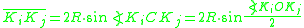
Therefore,

and substituting these in the formula above:

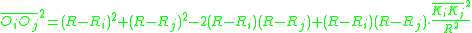

And finally, the length we seek is
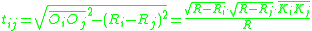
We can now evaluate the left hand side, with the help of the original Ptolemy's theorem
applied to the inscribed quadrilateral
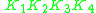 :
:
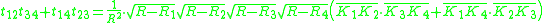
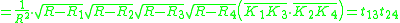
Q.E.D.
If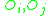 are both tangent from the same side of
are both tangent from the same side of 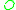 (both in or both out),
(both in or both out), 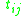 is the length of the exterior common tangent.
is the length of the exterior common tangent.
If are tangent from different sides of
are tangent from different sides of 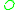 (one in and one out),
(one in and one out), 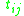 is the length of the interior common tangent.
is the length of the interior common tangent.
It is also worth noting that the converse of this statement is also true. That is, if equality holds, the circles are tangent.
.
For example, the shortest known proof of Feuerbach's theorem uses the converse theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Casey's theorem, also known as the generalized Ptolemy's theorem
Ptolemy's theorem
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral . The theorem is named after the Greek astronomer and mathematician Ptolemy...
, is a theorem in Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
named after the Irish mathematician
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
John Casey
John Casey (mathematician)
John Casey was a respected Irish geometer. He is most famous for Casey's theorem on a circle that is tangent to four other circles, an extension of the problem of Apollonius. However, he contributed several novel proofs and perspectives on Euclidean geometry...
.
Formulation of the theorem

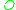 be a circle of radius
be a circle of radius 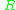 . Let
. Let 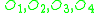 be (in that order) four non-intersecting circles that lie inside
be (in that order) four non-intersecting circles that lie inside  and tangent to it. Denote by
and tangent to it. Denote by 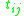 the length of the exterior common tangent of the circles
the length of the exterior common tangent of the circles 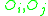 . Then:
. Then:
Note that in the degenerate case, where all four circles reduce to points, this is exactly Ptolemy's theorem
Ptolemy's theorem
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral . The theorem is named after the Greek astronomer and mathematician Ptolemy...
.
Proof
The following proof is due to Zacharias. Denote the radius of circle by
by 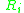 and its tangency point with the circle
and its tangency point with the circle 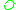 by
by 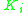 . We will use the notation
. We will use the notation 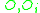 for the centers of the circles.
for the centers of the circles.Note that from Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
,
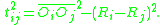
We will try to express this length in terms of the points
 . By the law of cosines
. By the law of cosinesLaw of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
in triangle
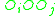 ,
,
Since the circles
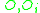 tangent to each other:
tangent to each other:
Let
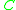 be a point on the circle
be a point on the circle  . According to the law of sines
. According to the law of sinesLaw of sines
In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
in triangle
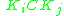 :
: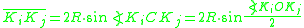
Therefore,

and substituting these in the formula above:

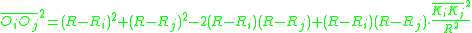

And finally, the length we seek is
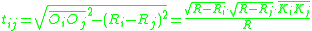
We can now evaluate the left hand side, with the help of the original Ptolemy's theorem
Ptolemy's theorem
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral . The theorem is named after the Greek astronomer and mathematician Ptolemy...
applied to the inscribed quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
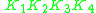 :
: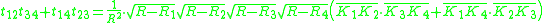
Q.E.D.
Further generalizations
It can be seen that the four circles need not lie inside the big circle. In fact, they may be tangent to it from the outside as well. In that case, the following change should be made:If
 are both tangent from the same side of
are both tangent from the same side of  (both in or both out),
(both in or both out), 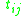 is the length of the exterior common tangent.
is the length of the exterior common tangent.If
 are tangent from different sides of
are tangent from different sides of 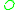 (one in and one out),
(one in and one out), 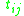 is the length of the interior common tangent.
is the length of the interior common tangent.It is also worth noting that the converse of this statement is also true. That is, if equality holds, the circles are tangent.
Applications
Casey's theorem and its converse can be used to prove a variety of statements in Euclidean geometryEuclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
.
For example, the shortest known proof of Feuerbach's theorem uses the converse theorem.

