Castigliano's method
Encyclopedia
Castigliano's method, named for Carlo Alberto Castigliano
, is a method for determining the displacements of a linear-elastic
system based on the partial derivative
s of the strain energy
. In the mathematics of structures, he is known for his two theorems:
Castigliano's method for calculating forces is an application of his first theorem, which states:
In equation form,
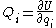
where U is the strain energy.
Castigliano's method for calculating displacements is an application of his second theorem, which states:
As above this can also be expressed as:
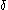can be found by Castigliano's second theorem :
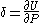
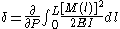
where E is Young's Modulus and I is the second moment of area of the cross-section, and M is the expression for the internal moment at point l therefore:
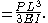
The result is the standard formula given for cantilever beams under end loads.
Carlo Alberto Castigliano
Carlo Alberto Castigliano was an Italian mathematician and physicist known for Castigliano's method for determining displacements in a linear-elastic system based on the partial derivatives of strain energy....
, is a method for determining the displacements of a linear-elastic
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
system based on the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of the strain energy
Energy principles in structural mechanics
Energy principles in structural mechanics express the relationships between stresses, strains or deformations, displacements, material properties, and external effects in the form of energy or work done by internal and external forces...
. In the mathematics of structures, he is known for his two theorems:
- Castigliano's first theorem – for forces in an elastic structure
- Castigliano's second theorem – for displacements in a linearly elastic structure.
Castigliano's method for calculating forces is an application of his first theorem, which states:
- If the strain energy of an elastic structure can be expressed as a function of generalised displacement qi; then the partial derivative of the strain energy with respect to generalised displacement gives the generalised force Qi.
In equation form,
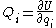
where U is the strain energy.
Castigliano's method for calculating displacements is an application of his second theorem, which states:
- If the strain energy of a linearly elastic structure can be expressed as a function of generalised force Qi; then the partial derivative of the strain energy with respect to generalised force gives the generalised displacement qi in the direction of Qi.
As above this can also be expressed as:
Examples
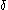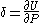
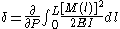
For a thin, straight cantilever beam with a load P at the end, the displacement can be found by Castigliano's second theorem :where E is Young's Modulus and I is the second moment of area of the cross-section, and M is the expression for the internal moment at point l therefore:
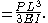
The result is the standard formula given for cantilever beams under end loads.
External links
- Carlo Alberto Castigliano
- Castigliano's theorems module of Wikibooks
- Castigliano's method: some examples – German language page
- Castigliano's method: some examples – Google's translation of the above German language page