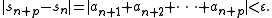Cauchy's convergence test
Encyclopedia
The Cauchy convergence test is a method used to test infinite series
for convergence. A series
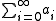
with real
or complex
summands ai is convergent if and only if for every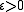 there is a natural number
there is a natural number
N such that
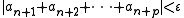
holds for all and .
The test works because the space R of real numbers and the space C of complex numbers (with the metric given by the absolute value) are both complete, so that the series is convergent if and only if
the partial sum
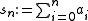
is a Cauchy sequence
: for every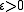 there is a number N, such that for all n, m > N holds
there is a number N, such that for all n, m > N holds

We can assume m > n and thus set p = m - n. The series is convergent if and only if
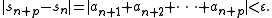
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
for convergence. A series
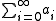
with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
summands ai is convergent if and only if for every
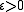 there is a natural number
there is a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
N such that
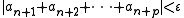
holds for all and .
The test works because the space R of real numbers and the space C of complex numbers (with the metric given by the absolute value) are both complete, so that the series is convergent if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the partial sum
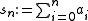
is a Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
: for every
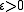 there is a number N, such that for all n, m > N holds
there is a number N, such that for all n, m > N holds
We can assume m > n and thus set p = m - n. The series is convergent if and only if