
Cauchy's equation
Encyclopedia
Cauchy's equation is an empirical relationship
between the refractive index
and wavelength
of light for a particular transparent material. It is named for the mathematician Augustin Louis Cauchy
, who defined it in 1836.
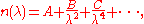
where n is the refractive index, λ is the wavelength, A, B, C, etc., are coefficient
s that can be determined for a material by fitting the equation to measured refractive indices at known wavelengths. The coefficients are usually quoted for λ as the vacuum wavelength in micrometre
s.
Usually, it is sufficient to use a two-term form of the equation:

where the coefficients A and B are determined specifically for this form of the equation.
A table of coefficients for common optical materials is shown below:
The theory of light-matter interaction on which Cauchy based this equation was later found to be incorrect. In particular, the equation is only valid for regions of normal dispersion
in the visible wavelength region. In the infrared
, the equation becomes inaccurate, and it cannot represent regions of anomalous dispersion. Despite this, its mathematical simplicity makes it useful in some applications.
The Sellmeier equation
is a later development of Cauchy's work that handles anomalously dispersive regions, and more accurately models a material's refractive index across the ultraviolet
, visible, and infrared spectrum.
Empirical relationship
In science, an empirical relationship is one based solely on observation rather than theory. An empirical relationship requires only confirmatory data irrespective of theoretical basis. Sometimes theoretical explanations for what were initially empirical relationships are found, in which case the...
between the refractive index
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
and wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of light for a particular transparent material. It is named for the mathematician Augustin Louis Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
, who defined it in 1836.
The equation
The most general form of Cauchy's equation is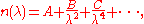
where n is the refractive index, λ is the wavelength, A, B, C, etc., are coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s that can be determined for a material by fitting the equation to measured refractive indices at known wavelengths. The coefficients are usually quoted for λ as the vacuum wavelength in micrometre
Micrometre
A micrometer , is by definition 1×10-6 of a meter .In plain English, it means one-millionth of a meter . Its unit symbol in the International System of Units is μm...
s.
Usually, it is sufficient to use a two-term form of the equation:

where the coefficients A and B are determined specifically for this form of the equation.
A table of coefficients for common optical materials is shown below:
| Material | A | B (μm2) |
| Fused silica | 1.4580 | 0.00354 |
| Borosilicate glass BK7 | 1.5046 | 0.00420 |
| Hard crown glass K5 | 1.5220 | 0.00459 |
| Barium crown glass BaK4 | 1.5690 | 0.00531 |
| Barium flint glass BaF10 | 1.6700 | 0.00743 |
| Dense flint glass SF10 | 1.7280 | 0.01342 |
The theory of light-matter interaction on which Cauchy based this equation was later found to be incorrect. In particular, the equation is only valid for regions of normal dispersion
Dispersion (optics)
In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
in the visible wavelength region. In the infrared
Infrared
Infrared light is electromagnetic radiation with a wavelength longer than that of visible light, measured from the nominal edge of visible red light at 0.74 micrometres , and extending conventionally to 300 µm...
, the equation becomes inaccurate, and it cannot represent regions of anomalous dispersion. Despite this, its mathematical simplicity makes it useful in some applications.
The Sellmeier equation
Sellmeier equation
The Sellmeier equation is an empirical relationship between refractive index and wavelength for a particular transparent medium. The equation is used to determine the dispersion of light in the medium....
is a later development of Cauchy's work that handles anomalously dispersive regions, and more accurately models a material's refractive index across the ultraviolet
Ultraviolet
Ultraviolet light is electromagnetic radiation with a wavelength shorter than that of visible light, but longer than X-rays, in the range 10 nm to 400 nm, and energies from 3 eV to 124 eV...
, visible, and infrared spectrum.

