Ceva's theorem is a theorem about triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

s in plane geometry

Plane geometry

In mathematics, plane geometry may refer to:*Euclidean plane geometry, the geometry of plane figures,*geometry of a plane,or sometimes:*geometry of a projective plane, most commonly the real projective plane but possibly the complex projective plane, Fano plane or others;*geometry of the hyperbolic...

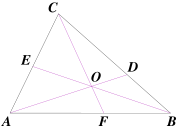
. Given a triangle ABC, let the lines AO, BO and CO be drawn from the vertices to a common point O to meet opposite sides at D, E and F respectively. Then
This equation uses signed lengths of segments, in other words the length AB is taken to be positive or negative according to whether A is to the left or right of B in some fixed orientation of the line. For example, AF/FB is defined as having positive value when F is between A and B and negative otherwise.

The converse is also true: If points D, E and F are chosen on BC, AC and AB respectively so that

then AD, BE and CF are concurrent

Concurrent lines

In geometry, two or more lines are said to be concurrent if they intersect at a single point.In a triangle, four basic types of sets of concurrent lines are altitudes, angle bisectors, medians, and perpendicular bisectors:...

. The converse is often included as part of the theorem.

The theorem is often attributed to Giovanni Ceva

Giovanni Ceva

Giovanni Ceva was an Italian mathematician widely known for proving Ceva's theorem in elementary geometry. His brother, Tommaso Ceva was also a well known poet and mathematician....

, who published it in his 1678 work De lineis rectis. But it was proven much earlier by Yusuf Al-Mu'taman ibn Hűd, an eleventh-century king of Zaragoza

Zaragoza

Zaragoza , also called Saragossa in English, is the capital city of the Zaragoza Province and of the autonomous community of Aragon, Spain...

.

Associated with the figures are several terms derived from Ceva's name: cevian (the lines AD, BE, CF are the cevians of O), cevian triangle (the triangle DEF is the cevian triangle of O); cevian nest, anticevian triangle, Ceva conjugate. (Ceva is pronounced Chay'va; cevian is pronounced chev'ian.)

The theorem is very similar to Menelaus' theorem

Menelaus' theorem

Menelaus' theorem, named for Menelaus of Alexandria, is a theorem about triangles in plane geometry. Given a triangle ABC, and a transversal line that crosses BC, AC and AB at points D, E and F respectively, with D, E, and F distinct from A, B and C, thenThis equation uses signed lengths of...

 in that their equations differ only in sign.

Proof of the theorem

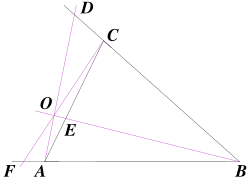
A standard proof is as follows:

First, the sign of the left-hand side is positive since either all three of the ratios are positive, the case where O is inside the triangle (upper diagram), or one is positive and the other two are negative, the case O is outside the triangle (lower diagram shows one case).

To check the magnitude, note that the area of a triangle of a given height is proportional to its base. So

Therefore,
(Replace the minus with a plus if A and O are on opposite sides of BC.)
Similarly,

and

Multiplying these three equations gives

as required.

The theorem can also be proven easily using Manelaus' theorem. From the transversal BOE of triangle ACF,

and from the From the transversal AOD of triangle BCF,

The theorem follows by dividing these two equations.

The converse follows as a corollary. Let D, E and F be given on the lines BC, AC and AB so that the equation holds. Let AD and BE meet at O and let F′ be the point where FO crosses AB. Then by the theorem, the equation also holds for D, E and F′. Comparing the two,

But at most one point can cut a segment in a given ratio so F=F′.

Generalizations

The theorem can be generalized to higher dimensional simplex

Simplex

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

es using barycentric coordinates

Barycentric coordinates (mathematics)

In geometry, the barycentric coordinate system is a coordinate system in which the location of a point is specified as the center of mass, or barycenter, of masses placed at the vertices of a simplex . Barycentric coordinates are a form of homogeneous coordinates...

. Define a cevian of an n-simplex as a ray from each vertex to a point on the opposite (n-1)-face (facet

Facet (mathematics)

A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...

). Then the cevians are concurrent if and only if a mass distribution

Mass distribution

Mass distribution is a term used in physics and mechanics and describes the spatial distribution of mass within a solid body. In principle, it is relevant also for gases or liquids, but on earth their mass distribution is almost homogeneous.-Astronomy:...

 can be assigned to the vertices such that each cevian intersects the opposite facet at its center of mass

Center of mass

In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...

. Moreover, the intersection point of the cevians is the center of mass of the simplex. (Landy. See Wernicke for an earlier result.)

Routh's theorem

Routh's theorem

In geometry, Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the intersection of three cevians...

 gives the area of the triangle formed by three cevians in the case that they are not concurrent. Ceva's theorem can be obtained from it by setting the area equal to zero and solving.

The analogue of the theorem for general polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

s in the plane has been known since the early nineteenth century . The theorem has also been generalized to triangles on other surfaces of constant curvature

Constant curvature

In mathematics, constant curvature in differential geometry is a concept most commonly applied to surfaces. For those the scalar curvature is a single number determining the local geometry, and its constancy has the obvious meaning that it is the same at all points...

 (Masal'tsev 1994).

External links

• Menelaus and Ceva at MathPages
• Derivations and applications of Ceva's Theorem at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
  
  
• Trigonometric Form of Ceva's Theorem at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
  
  
• Glossary of Encyclopedia of Triangle Centers includes definitions of cevian triangle, cevian nest, anticevian triangle, Ceva conjugate, and cevapoint
• Conics Associated with a Cevian Nest, by Clark Kimberling
• Ceva's Theorem by Jay Warendorff, Wolfram Demonstrations Project
  Wolfram Demonstrations Project
  The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
  
  .