
Chebychev–Grübler–Kutzbach criterion
Encyclopedia
The Chebychev
–Grübler–Kutzbach criterion determines the degree of freedom of a kinematic chain
, that is, a coupling of rigid bodies by means of mechanical constraints. These devices are also called linkage
s.
The Kutzbach criterion is also called the mobility formula, because it computes the number of parameters that define the configuration of a linkage from the number of links and joints and the degree of freedom at each joint.
Interesting and useful linkages have been designed that violate the mobility formula by using special geometric features and dimensions to provide more mobility than would by predicted by this formula. These devices are called overconstrained mechanisms.
A system of n rigid bodies moving in space has 6n degrees of freedom measured relative to a fixed frame. This frame is included in the count of bodies, so that mobility is independent of the choice of the link that will form the fixed frame. Then the degree-of-freedom of this system is M=6(N-1), where N=n+1 is the number of moving bodies plus the fixed body.
Joints that connect bodies in this system remove degrees of freedom and reduce mobility. Specifically, hinges and sliders each impose five constraints and therefore remove five degrees of freedom. It is convenient to define the number of constraints c that a joint imposes in terms of the joint's freedom f, where c=6-f. In the case of a hinge or slider, which are one degree of freedom joints, have f=1 and therefore c=6-1=5.
The result is that the mobility of a system formed from n moving links and j joints each with freedom fi, i=1, ..., j, is given by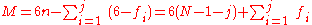
Recall that N includes the fixed link.
There are two important special cases: (i) a simple open chain, and (ii) a simple closed chain. A single open chain consists of n moving links connected end to end by j joints, with one end connected to a ground link. Thus, in this case N=j+1 and the mobility of the chain is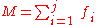
For a simple closed chain, n moving links are connected end-to-end by n+1 joints such that the two ends are connected to the ground link forming a loop. In this case, we have N=j and the mobility of the chain is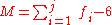
An example of a simple open chain is a serial robot manipulator. These robotic systems are constructed from a series of links connected by six one degree-of-freedom revolute or prismatic joints, so the system has six degrees of freedom.
An example of a simple closed chain is the RSSR spatial four-bar linkage. The sum of the freedom of these joints is eight, so the mobility of the linkage is two, where one of the degrees of freedom is the rotation of the coupler around the line joining the two S joints.
so that the movement of all of the bodies are constrained to lie on parallel planes, to form what is known as a planar linkage. It is also possible to construct the linkage system so that all of the bodies move on concentric spheres, forming a spherical linkage. In both cases, the degrees of freedom of the links in each system is now three rather than six, and the constraints imposed by joints are now c=3-f.
In this case, the mobility formula is given by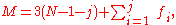
and the special cases become
An example of a planar simple closed chain is the planar four-bar linkage, which is a four-bar loop with four one degree-of-freedom joints and therefore has mobility M=1.
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
–Grübler–Kutzbach criterion determines the degree of freedom of a kinematic chain
Kinematic chain
A kinematic chain is the assembly of several kinematic pairs connecting rigid body segments. The complexity of the chain is determined by the following factors:...
, that is, a coupling of rigid bodies by means of mechanical constraints. These devices are also called linkage
Linkage (mechanical)
A mechanical linkage is an assembly of bodies connected together to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for...
s.
The Kutzbach criterion is also called the mobility formula, because it computes the number of parameters that define the configuration of a linkage from the number of links and joints and the degree of freedom at each joint.
Interesting and useful linkages have been designed that violate the mobility formula by using special geometric features and dimensions to provide more mobility than would by predicted by this formula. These devices are called overconstrained mechanisms.
Mobility formula
The mobility formula counts the number of parameters that define the positions of a set of rigid bodies and then reduces this number by the constraints that are imposed by joints connecting these bodies.A system of n rigid bodies moving in space has 6n degrees of freedom measured relative to a fixed frame. This frame is included in the count of bodies, so that mobility is independent of the choice of the link that will form the fixed frame. Then the degree-of-freedom of this system is M=6(N-1), where N=n+1 is the number of moving bodies plus the fixed body.
Joints that connect bodies in this system remove degrees of freedom and reduce mobility. Specifically, hinges and sliders each impose five constraints and therefore remove five degrees of freedom. It is convenient to define the number of constraints c that a joint imposes in terms of the joint's freedom f, where c=6-f. In the case of a hinge or slider, which are one degree of freedom joints, have f=1 and therefore c=6-1=5.
The result is that the mobility of a system formed from n moving links and j joints each with freedom fi, i=1, ..., j, is given by
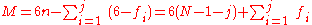
Recall that N includes the fixed link.
There are two important special cases: (i) a simple open chain, and (ii) a simple closed chain. A single open chain consists of n moving links connected end to end by j joints, with one end connected to a ground link. Thus, in this case N=j+1 and the mobility of the chain is
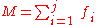
For a simple closed chain, n moving links are connected end-to-end by n+1 joints such that the two ends are connected to the ground link forming a loop. In this case, we have N=j and the mobility of the chain is
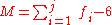
An example of a simple open chain is a serial robot manipulator. These robotic systems are constructed from a series of links connected by six one degree-of-freedom revolute or prismatic joints, so the system has six degrees of freedom.
An example of a simple closed chain is the RSSR spatial four-bar linkage. The sum of the freedom of these joints is eight, so the mobility of the linkage is two, where one of the degrees of freedom is the rotation of the coupler around the line joining the two S joints.
Planar and spherical movement
It is common practice to design the linkage systemLinkage (mechanical)
A mechanical linkage is an assembly of bodies connected together to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for...
so that the movement of all of the bodies are constrained to lie on parallel planes, to form what is known as a planar linkage. It is also possible to construct the linkage system so that all of the bodies move on concentric spheres, forming a spherical linkage. In both cases, the degrees of freedom of the links in each system is now three rather than six, and the constraints imposed by joints are now c=3-f.
In this case, the mobility formula is given by
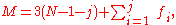
and the special cases become
- planar or spherical simple open chain,
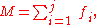
- planar or spherical simple closed chain,
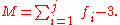
An example of a planar simple closed chain is the planar four-bar linkage, which is a four-bar loop with four one degree-of-freedom joints and therefore has mobility M=1.
See also
- Overconstrained mechanism
- Four-bar linkage
- Linkage (mechanical)Linkage (mechanical)A mechanical linkage is an assembly of bodies connected together to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for...
- Burmester theory
- Machine (mechanical)Machine (mechanical)The mechanical properties of a machine manage power to achieve desired forces and movement. Modern machines often include computers and sensors that monitor performance and plan movement, and are called mechanical systems....
- Mechanical systemMechanical systemA mechanical system manages power to accomplish a task that involves forces and movement. Mechanical is derived from the Latin word machina, which in turn derives from the Doric Greek μαχανά , Ionic Greek μηχανή "contrivance, machine, engine" and that from μῆχος , "means, expedient, remedy".The...

