
Chebyshev's bias
Encyclopedia
In prime number theory
, Chebyshev's bias is the phenomenon that most of the time, there are more primes of the form 4k + 3 than of the form 4k + 1, up to the same limit. This phenomenon was first observed by Chebyshev
in 1853.
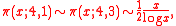
i.e., half of the primes are of the form 4k+1, and half of the form 4k + 3. A reasonable guess would be that π(x;4,1)>π(x; 4, 3) and π(x; 4, 1) < π(x; 4, 3) each also occur 50 % of the time. This, however, is not supported by numerical evidence—in fact, π(x,4,3)>π(x;4,1) occurs much more frequently.
In general, if 0 < a,b < q are integers, (a, q) = (b, q) = 1, a is a quadratic residue, b is a quadratic nonresidue mod q, then π(x; q, b) > π(x; q, a) occurs more often than not. This has been proved only by assuming strong forms of the Riemann hypothesis
. The conjecture of Knapowski and Turán
, however, that the density of the numbers x for which π(x; 4, 3) > π(x; 4, 1) holds, is 1, turned out to be false. They, however, do have a logarithmic density
, which is approximately 0.9959...(Rubinstein—Sarnak, 1994).
Prime number theory
Prime number theory may refer to:* Prime number* Prime number theorem* Number theory...
, Chebyshev's bias is the phenomenon that most of the time, there are more primes of the form 4k + 3 than of the form 4k + 1, up to the same limit. This phenomenon was first observed by Chebyshev
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
in 1853.
Description
Let π(x; 4, 1) denote the number of primes of the form 4k + 1 up to x. Similarly, let π(x; 4, 3) denote the number of primes of the form 4k + 3 up to x. By the prime number theorem, extended to arithmetic progression,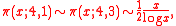
i.e., half of the primes are of the form 4k+1, and half of the form 4k + 3. A reasonable guess would be that π(x;4,1)>π(x; 4, 3) and π(x; 4, 1) < π(x; 4, 3) each also occur 50 % of the time. This, however, is not supported by numerical evidence—in fact, π(x,4,3)>π(x;4,1) occurs much more frequently.
In general, if 0 < a,b < q are integers, (a, q) = (b, q) = 1, a is a quadratic residue, b is a quadratic nonresidue mod q, then π(x; q, b) > π(x; q, a) occurs more often than not. This has been proved only by assuming strong forms of the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
. The conjecture of Knapowski and Turán
Pál Turán
Paul Turán was a Hungarian mathematician who worked primarily in number theory. He had a long collaboration with fellow Hungarian mathematician Paul Erdős, lasting 46 years and resulting in 28 joint papers.- Life and education :...
, however, that the density of the numbers x for which π(x; 4, 3) > π(x; 4, 1) holds, is 1, turned out to be false. They, however, do have a logarithmic density
Natural density
In number theory, asymptotic density is one of the possibilities to measure how large a subset of the set of natural numbers is....
, which is approximately 0.9959...(Rubinstein—Sarnak, 1994).

