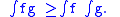Chebyshev's sum inequality
Encyclopedia
In mathematics
, Chebyshev's sum inequality, named after Pafnuty Chebyshev
, states that if
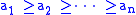
and

then
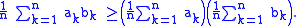
Similarly, if
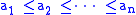
and

then
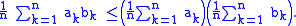
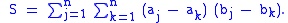
The two sequences are non-increasing, therefore and have the same sign for any . Hence .
Opening the brackets, we deduce:
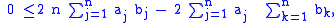
whence
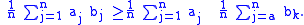
An alternative proof is simply obtained with the rearrangement inequality.
If f and g are real-valued, integrable functions over [0, 1], both increasing or both decreasing, then
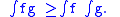
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Chebyshev's sum inequality, named after Pafnuty Chebyshev
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
, states that if
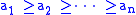
and

then
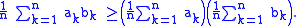
Similarly, if
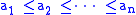
and

then
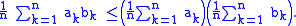
Proof
Consider the sum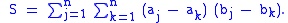
The two sequences are non-increasing, therefore and have the same sign for any . Hence .
Opening the brackets, we deduce:
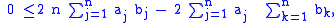
whence
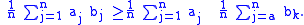
An alternative proof is simply obtained with the rearrangement inequality.
Continuous version
There is also a continuous version of Chebyshev's sum inequality:If f and g are real-valued, integrable functions over [0, 1], both increasing or both decreasing, then