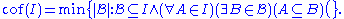Cichon's diagram
Encyclopedia
In set theory,
Cichoń's diagram or Cichon's diagram is a table of 10 infinite cardinal number
s related to the set theory of the reals displaying the provable relations between these cardinal invariants. All these cardinals are greater than or equal to , the smallest uncountable cardinal, and they are bounded above by
, the smallest uncountable cardinal, and they are bounded above by 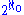 , the cardinality of the continuum
, the cardinality of the continuum
. Four cardinals describe properties of the ideal
of sets of measure zero
; four more describe the corresponding properties of the ideal of meager sets (first category sets)
.
of a fixed infinite set X, containing all finite subsets of X. We define the following "cardinal coefficients" of I:
Furthermore, the "bounding number" or "unboundedness number"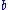 and the "dominating number"
and the "dominating number" 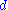 are defined as follows:
are defined as follows:
where "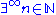 " means: "there are infinitely many natural numbers n such that...", and "
" means: "there are infinitely many natural numbers n such that...", and "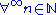 " means "for all except finitely many natural numbers n we have...".
" means "for all except finitely many natural numbers n we have...".
 be the σ-ideal of those subsets of the real line which are meager (or "of the first category") in the euclidean topology
be the σ-ideal of those subsets of the real line which are meager (or "of the first category") in the euclidean topology
, and let
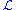 be the σ-ideal of those subsets of the real line which are of Lebesgue measure
be the σ-ideal of those subsets of the real line which are of Lebesgue measure
zero. Then the following inequalities hold (where an arrow from to is to be read as meaning that ):
In addition, the following relations hold:
 and
and
 .
.
It turns out that the inequalities described by the diagram, together with the relations mentioned above, are all the relations between these cardinals that are provable in ZFC, in the following sense. Let A be any assignment of the cardinals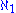 and
and 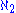 to the 10 cardinals in Cichoń's diagram. Then, if A is consistent with the diagram in that there is no arrow from
to the 10 cardinals in Cichoń's diagram. Then, if A is consistent with the diagram in that there is no arrow from 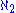 to
to  , and if A also satisfies the two additional relations, then A can be realized in some model of ZFC.
, and if A also satisfies the two additional relations, then A can be realized in some model of ZFC.
Some inequalities in the diagram (such as "add ≤ cov") follow immediately from the definitions. The inequalities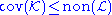 and
and
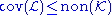 are classical theorems
are classical theorems
and follow from the fact that the real line can be partitioned into a meager set and a set of measure zero.
The continuum hypothesis
, of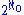 being equal to
being equal to 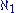 , would make all of these arrows equalities.
, would make all of these arrows equalities.
Martin's axiom
, a weakening of CH, implies that all cardinals in the diagram (except perhaps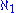 ) are equal to
) are equal to  .
.
Cichoń's diagram or Cichon's diagram is a table of 10 infinite cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s related to the set theory of the reals displaying the provable relations between these cardinal invariants. All these cardinals are greater than or equal to
 , the smallest uncountable cardinal, and they are bounded above by
, the smallest uncountable cardinal, and they are bounded above by 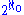 , the cardinality of the continuum
, the cardinality of the continuumCardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
. Four cardinals describe properties of the ideal
Ideal (order theory)
In mathematical order theory, an ideal is a special subset of a partially ordered set . Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion...
of sets of measure zero
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
; four more describe the corresponding properties of the ideal of meager sets (first category sets)
Meagre set
In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
.
Definitions
Let I be an idealIdeal (set theory)
In the mathematical field of set theory, an ideal is a collection of sets that are considered to be "small" or "negligible". Every subset of an element of the ideal must also be in the ideal , and the union of any two elements of the ideal must also be in the ideal.More formally, given a set X, an...
of a fixed infinite set X, containing all finite subsets of X. We define the following "cardinal coefficients" of I:
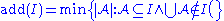 .
.
-
- The "additivity" of I is the smallest number of sets from I whose union is not in I any more. As any ideal is closed under finite unions, this number is always at least
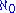 ; if I is a σ-ideal, then add(I)≥
; if I is a σ-ideal, then add(I)≥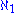 .
.
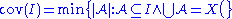 .
.
- The "covering number" of I is the smallest number of sets from I whose union is all of X. As X itself is not in I, we must have add(I) ≤ cov(I).
 ,
,
- The "uniformity number" of I (sometimes also written
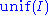 ) is the size of the smallest set not in I. By our assumption on I, add(I) ≤ non(I).
) is the size of the smallest set not in I. By our assumption on I, add(I) ≤ non(I).
- The "cofinality" of I is the cofinalityCofinalityIn mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
of the partial order (I, ⊆). It is easy to see that we must have non(I) ≤ cof(I) and cov(I) ≤ cof(I).
- The "additivity" of I is the smallest number of sets from I whose union is not in I any more. As any ideal is closed under finite unions, this number is always at least
Furthermore, the "bounding number" or "unboundedness number"
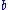 and the "dominating number"
and the "dominating number" 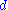 are defined as follows:
are defined as follows:
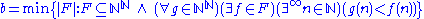 ,
, ,
,
where "
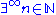 " means: "there are infinitely many natural numbers n such that...", and "
" means: "there are infinitely many natural numbers n such that...", and "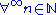 " means "for all except finitely many natural numbers n we have...".
" means "for all except finitely many natural numbers n we have...".Diagram
Let be the σ-ideal of those subsets of the real line which are meager (or "of the first category") in the euclidean topology
be the σ-ideal of those subsets of the real line which are meager (or "of the first category") in the euclidean topologyEuclidean topology
In mathematics, and especially general topology, the Euclidean topology is an example of a topology given to the set of real numbers, denoted by R...
, and let
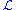 be the σ-ideal of those subsets of the real line which are of Lebesgue measure
be the σ-ideal of those subsets of the real line which are of Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero. Then the following inequalities hold (where an arrow from to is to be read as meaning that ):
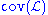 |
 |
 |
 |
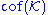 |
 |
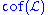 |
 |
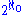 |
||
 |
 |
 |
 |
|||||||
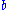 |
 |
 |
||||||||
 |
 |
|||||||||
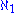 |
 |
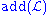 |
 |
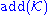 |
 |
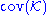 |
 |
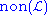 |
In addition, the following relations hold:
 and
and .
.It turns out that the inequalities described by the diagram, together with the relations mentioned above, are all the relations between these cardinals that are provable in ZFC, in the following sense. Let A be any assignment of the cardinals
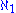 and
and 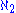 to the 10 cardinals in Cichoń's diagram. Then, if A is consistent with the diagram in that there is no arrow from
to the 10 cardinals in Cichoń's diagram. Then, if A is consistent with the diagram in that there is no arrow from 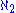 to
to  , and if A also satisfies the two additional relations, then A can be realized in some model of ZFC.
, and if A also satisfies the two additional relations, then A can be realized in some model of ZFC.Some inequalities in the diagram (such as "add ≤ cov") follow immediately from the definitions. The inequalities
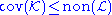 and
and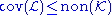 are classical theorems
are classical theoremsand follow from the fact that the real line can be partitioned into a meager set and a set of measure zero.
Remarks
The British mathematician David Fremlin named the diagram after the Wrocław mathematician Jacek Cichoń.The continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
, of
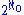 being equal to
being equal to 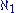 , would make all of these arrows equalities.
, would make all of these arrows equalities.Martin's axiom
Martin's axiom
In the mathematical field of set theory, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH...
, a weakening of CH, implies that all cardinals in the diagram (except perhaps
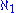 ) are equal to
) are equal to  .
.