
Codd's cellular automaton
Encyclopedia
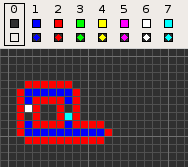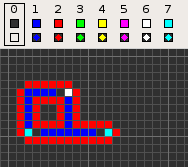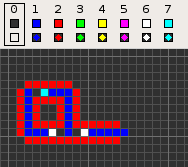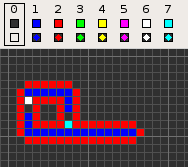
Cellular automaton
A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
(CA) devised by the British
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
computer scientist
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
Edgar F. Codd
Edgar F. Codd
Edgar Frank "Ted" Codd was an English computer scientist who, while working for IBM, invented the relational model for database management, the theoretical basis for relational databases...
in 1968. It was designed to recreate the computation- and construction-universality of von Neumann's CA but with fewer states: 8 instead of 29. Codd showed that it was possible to make a self-reproducing machine in his CA, in a similar way to von Neumann's universal constructor
Von Neumann universal constructor
John von Neumann's Universal Constructor is a self-replicating machine in a cellular automata environment. It was designed in the 1940s, without the use of a computer. The fundamental details of the machine were published in von Neumann's book Theory of Self-Reproducing Automata, completed in...
but never gave a complete implementation.
Historical Context
In the 1940s and 50's, John von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
posed the following problem:
- What kind of logical organization is sufficient for an automaton to be able to reproduce itself?
He was able to construct a Universal Constructor
Von Neumann universal constructor
John von Neumann's Universal Constructor is a self-replicating machine in a cellular automata environment. It was designed in the 1940s, without the use of a computer. The fundamental details of the machine were published in von Neumann's book Theory of Self-Reproducing Automata, completed in...
with a square grid and 29 states. E.F. Codd found a simpler machine with only eight states. Therefore von Neumann's question had to be modified:
- What kind of logical organization is necessary for an automaton to be able to reproduce itself?
Three years after Codd's work, Edwin Roger Banks showed a 4-state CA (appendix IV in his thesis) that was also computation- and construction-universal but again didn't implement a self-reproducing machine.
John Devore, in his 1973 master's thesis, was able to greatly reduce the size of Codd's machine design while using almost the same 8-state CA. More than just a theoretical device, Devore's machine was possibly the first implementation of a self-reproducing CA. The machine itself could fit inside computer memory but the data tape stretched for thousands of cells, so simulation of the entire self-reproduction cycle was not possible. Decades later, Devore's original design would complete self-reproduction in simulation using the Golly program.
In 1984, Christopher Langton
Christopher Langton
Christopher Langton is an American computer scientist and one of the founders of the field of artificial life. He coined the term in the late 1980s when he organized the first "Workshop on the Synthesis and Simulation of Living Systems" at the Los Alamos National Laboratory in 1987.Langton made...
extended Codd's cellular automaton to create Langton's loops
Langton's loops
Langton's loops are a particular "species" of artificial life in a cellular automaton created in 1984 by Christopher Langton. They consist of a loop of cells containing genetic information, which flows continuously around the loop and out along an "arm" , which will become the daughter loop...
, which also exhibits reproductive behavior but uses only a very small number of cells compared to the hundreds of thousands needed for self-reproduction in von Neumann, Codd or Banks' cellular automata.
Comparison of CA rulesets
| CA | number of states | symmetries | computation- and construction-universal | size of self-reproducing machine |
|---|---|---|---|---|
| von Neumann | 29 | none | yes | 130,622 cells |
| Codd | 8 | rotations | yes | 283,126,588 cells |
| Devore | 8 | rotations | yes | 94,794 cells |
| Banks-IV | 4 | rotations and reflections | yes | unknown |
| Langton's loops | 8 | rotations | no | 86 cells |
Specification

Von Neumann neighborhood
In cellular automata, the von Neumann neighborhood comprises the four cells orthogonally surrounding a central cell on a two-dimensional square lattice. The neighborhood is named after John von Neumann, who used it for his pioneering cellular automata including the Universal Constructor...
with rotational symmetry.
The table below shows the signal-trains needed to accomplish different tasks. Some of the signal trains need to be separated by two blanks (state 1) on the wire to avoid interference, so the 'extend' signal-train used in the image at the top appears here as '70116011'.
| purpose | signal train |
|---|---|
| extend | 70116011 |
| extend_left | 4011401150116011 |
| extend_right | 5011501140116011 |
| retract | 4011501160116011 |
| retract_left | 5011601160116011 |
| retract_right | 4011601160116011 |
| mark | 701160114011501170116011 |
| erase | 601170114011501160116011 |
| sense | 70117011 |
| cap | 40116011 |
| inject_sheath | 701150116011 |
| inject_trigger | 60117011701160116011 |
Universal computer-constructor
Codd designed a self-replicating computer in the cellular automaton, based on Wang's W-machineWang B-machine
As presented by Hao Wang , his basic machine B is an extremely simple computational model equivalent to the Turing machine. It is "the first formulation of a Turing-machine theory in terms of computer-like models" . With only 4 sequential instructions it is very similar to, but even simpler than,...
. However, the design was so colossal that it evaded implementation until 2009, when Tim Hutton constructed an explicit configuration. There were some minor errors in Codd's design, so Hutton's implementation differs slightly, in both the configuration and the ruleset.
See also
- Artificial lifeArtificial lifeArtificial life is a field of study and an associated art form which examine systems related to life, its processes, and its evolution through simulations using computer models, robotics, and biochemistry. The discipline was named by Christopher Langton, an American computer scientist, in 1986...
- Cellular automatonCellular automatonA cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
- Conway's game of lifeConway's Game of LifeThe Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970....
- Langton's loopsLangton's loopsLangton's loops are a particular "species" of artificial life in a cellular automaton created in 1984 by Christopher Langton. They consist of a loop of cells containing genetic information, which flows continuously around the loop and out along an "arm" , which will become the daughter loop...
- von Neumann cellular automaton
- Wireworld
External links
- The Rule Table Repository has the transition table for Codd's CA.
- Golly - supports Codd's CA along with the Game of LifeConway's Game of LifeThe Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970....
, and other rulesets. - Download the complete machine (13MB) and more details.

