
Coxeter's loxodromic sequence of tangent circles
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Coxeter's loxodromic sequence of tangent circles is an infinite sequence of circles arranged such that any four consecutive circles in the sequence are pairwise mutually tangent. This means that each circle in the sequence is tangent to the three circles that precede it and also to the three circles that follow it.
The radii of the circles in the sequence form a geometric progression
Geometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
with ratio

where φ is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
. k and its reciprocal satisfy the equation
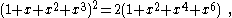
and so any four consecutive circles in the sequence meet the conditions of Descartes' theorem
Descartes' theorem
In geometry, Descartes' theorem, named after René Descartes, establishes a relationship between four kissing, or mutually tangent, circles. The theorem can be used to construct a fourth circle tangent to three given, mutually tangent circles.-History:...
.
The centres of the circles in the sequence lie on a logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
. Viewed from the centre of the spiral, the angle between the centres of successive circles is

The construction is named after geometer Donald Coxeter, who generalised the two-dimensional case to sequences of spheres and hypersphere
Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
s in higher dimensions.

