
Craig's theorem
Encyclopedia
In mathematical logic
, Craig's theorem states that any recursively enumerable set
of well-formed formula
s of a first-order language is (primitively) recursively axiomatizable. This result is not related to the well-known Craig interpolation
theorem.
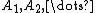 be an enumeration of the axioms of a recursively enumerable set T of first-order formulas. Construct another set T* consisting of
be an enumeration of the axioms of a recursively enumerable set T of first-order formulas. Construct another set T* consisting of

for each positive integer i. The deductive closures of T* and T are thus equivalent; the proof will show that T* is a decidable set. A decision procedure for T* lends itself according to the following informal reasoning. Each member of T* is either or of the form
or of the form

Since each formula has finite length, it is checkable whether or not it is or of the said form. If it is of the said form and consists of j conjuncts, it is in T* if it is the expression
or of the said form. If it is of the said form and consists of j conjuncts, it is in T* if it is the expression 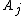 ; otherwise it is not in T*. Again, it is checkable whether it is in fact
; otherwise it is not in T*. Again, it is checkable whether it is in fact 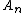 by going through the enumeration of the axioms of T and then checking symbol-for-symbol whether the expressions are identical.
by going through the enumeration of the axioms of T and then checking symbol-for-symbol whether the expressions are identical.
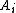 with
with

one instead replaces it with
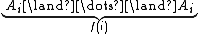 (*)
(*)
where f(x) is a function that, given i, returns a computation history showing that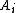 is in the original recursively enumerable set of axioms. It is possible for a primitive recursive function to parse an expression of form (*) to obtain
is in the original recursively enumerable set of axioms. It is possible for a primitive recursive function to parse an expression of form (*) to obtain 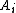 and j. Then, because Kleene's T predicate
and j. Then, because Kleene's T predicate
is primitive recursive, it is possible for a primitive recursive function to verify that j is indeed a computation history as required.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, Craig's theorem states that any recursively enumerable set
Recursively enumerable set
In computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
of well-formed formula
Well-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
s of a first-order language is (primitively) recursively axiomatizable. This result is not related to the well-known Craig interpolation
Craig interpolation
In mathematical logic, Craig's interpolation theorem is a result about the relationship between different logical theories. Roughly stated, the theorem says that if a formula φ implies a formula ψ then there is a third formula ρ, called an interpolant, such that every nonlogical symbol...
theorem.
Recursive axiomatization
Let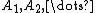 be an enumeration of the axioms of a recursively enumerable set T of first-order formulas. Construct another set T* consisting of
be an enumeration of the axioms of a recursively enumerable set T of first-order formulas. Construct another set T* consisting of
for each positive integer i. The deductive closures of T* and T are thus equivalent; the proof will show that T* is a decidable set. A decision procedure for T* lends itself according to the following informal reasoning. Each member of T* is either
 or of the form
or of the form
Since each formula has finite length, it is checkable whether or not it is
 or of the said form. If it is of the said form and consists of j conjuncts, it is in T* if it is the expression
or of the said form. If it is of the said form and consists of j conjuncts, it is in T* if it is the expression 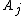 ; otherwise it is not in T*. Again, it is checkable whether it is in fact
; otherwise it is not in T*. Again, it is checkable whether it is in fact 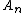 by going through the enumeration of the axioms of T and then checking symbol-for-symbol whether the expressions are identical.
by going through the enumeration of the axioms of T and then checking symbol-for-symbol whether the expressions are identical.Primitive recursive axiomatizations
The proof above shows that for each recursively enumerable set of axioms there is a recursive set of axioms with the same deductive closure. A set of axioms is primitive recursive if there is a primitive recursive function that decides membership in the set. To obtain a primitive recursive aximatization, instead of replacing a formula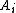 with
with
one instead replaces it with
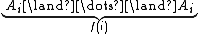 (*)
(*)where f(x) is a function that, given i, returns a computation history showing that
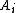 is in the original recursively enumerable set of axioms. It is possible for a primitive recursive function to parse an expression of form (*) to obtain
is in the original recursively enumerable set of axioms. It is possible for a primitive recursive function to parse an expression of form (*) to obtain 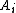 and j. Then, because Kleene's T predicate
and j. Then, because Kleene's T predicateKleene's T predicate
In computability theory, the T predicate, first studied by mathematician Stephen Cole Kleene, is a particular set of triples of natural numbers that is used to represent computable functions within formal theories of arithmetic...
is primitive recursive, it is possible for a primitive recursive function to verify that j is indeed a computation history as required.

