
Dickson's lemma
Encyclopedia
In mathematics
, Dickson's lemma is a finiteness statement applying to n-tuples of natural number
s. It is a simple fact from combinatorics
, which has become attributed to the American algebraist L. E. Dickson. It was certainly known earlier, for example to Gordan in his researches on invariant theory
.
Stating it first for clarity for N2, for any pair (m,n) of natural numbers we can introduce
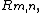
the 'rectangle' of numbers (r, s) with r at least m and s at least n. This is semi-infinite in the north and east directions, in the usual plane representation. The lemma then states that any union of the Rm,n can be expressed as the union of a finite subset of those Rm,n. This is analogous to the conventional topological definition of compactness
.
The generalization to Nk is the natural one, with k-tuples in place of pairs.
The statement says something about Nk as the topological space
with the product topology
arising from N, where the latter has the (semi-continuity
) topology in which the open sets are all sets Rm defined as all n with n at least m. The 'rectangles' are by definition a base for the topology; it says finite unions give all open sets.
As for the proof of the lemma, it can be derived directly, but a slick way is to show that it is a special case of Hilbert's basis theorem
. In fact it is essentially the case of ideals generated by monomial
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Dickson's lemma is a finiteness statement applying to n-tuples of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s. It is a simple fact from combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, which has become attributed to the American algebraist L. E. Dickson. It was certainly known earlier, for example to Gordan in his researches on invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
.
Stating it first for clarity for N2, for any pair (m,n) of natural numbers we can introduce
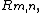
the 'rectangle' of numbers (r, s) with r at least m and s at least n. This is semi-infinite in the north and east directions, in the usual plane representation. The lemma then states that any union of the Rm,n can be expressed as the union of a finite subset of those Rm,n. This is analogous to the conventional topological definition of compactness
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
.
The generalization to Nk is the natural one, with k-tuples in place of pairs.
The statement says something about Nk as the topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
with the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
arising from N, where the latter has the (semi-continuity
Semi-continuity
In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
) topology in which the open sets are all sets Rm defined as all n with n at least m. The 'rectangles' are by definition a base for the topology; it says finite unions give all open sets.
As for the proof of the lemma, it can be derived directly, but a slick way is to show that it is a special case of Hilbert's basis theorem
Hilbert's basis theorem
In mathematics, specifically commutative algebra, Hilbert's basis theorem states that every ideal in the ring of multivariate polynomials over a Noetherian ring is finitely generated. This can be translated into algebraic geometry as follows: every algebraic set over a field can be described as the...
. In fact it is essentially the case of ideals generated by monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s.

