
Diner's dilemma
Encyclopedia
In game theory
, the Unscrupulous diner's dilemma (or just Diner's dilemma) is an n-player
prisoner's dilemma
. The situation imagined is that several individuals go out to eat, and prior to ordering they agree to split the check equally between all of them. Each individual must now choose whether to order the expensive or inexpensive dish. It is presupposed that the expensive dish is better than the cheaper, but not by enough to warrant paying the difference compared to eating alone. Each individual reasons that the expense they add to their bill by ordering the more expensive item is very small, and thus the improved dining experience is worth the money. However, every individual reasons this way and they all end up paying for the cost of the more expensive meal, which, by assumption, is worse for everyone than ordering and paying for the cheaper meal.
 . Also, in order to make the game sufficiently similar to the Prisoner's dilemma
. Also, in order to make the game sufficiently similar to the Prisoner's dilemma
we presume that one would prefer to order the expensive meal given others will help defray the cost,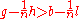
Consider an arbitrary set of strategies by a player's opponent. Let the total cost of the other player's meals be x. The cost of ordering the cheap meal is and the cost of ordering the expensive meal is
and the cost of ordering the expensive meal is  . So the utilities for each meal are
. So the utilities for each meal are 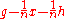 for the expensive meal and
for the expensive meal and  for the cheaper meal. By assumption, the utility of ordering the expensive meal is higher. Remember that the choice of opponents' strategies was arbitrary and that the situation is symmetric. This proves that the expensive meal is strictly dominant
for the cheaper meal. By assumption, the utility of ordering the expensive meal is higher. Remember that the choice of opponents' strategies was arbitrary and that the situation is symmetric. This proves that the expensive meal is strictly dominant
and thus the unique Nash equilibrium
.
If everyone orders the expensive meal all of the diners pay h and their total utility is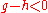 . On the other hand suppose that all the individuals had ordered the cheap meal, their utility would have been
. On the other hand suppose that all the individuals had ordered the cheap meal, their utility would have been 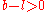 . This demonstrates the similarity between the Diner's dilemma and the Prisoner's dilemma. Like the Prisoner's dilemma, everyone is worse off by playing the unique equilibrium than they would have been if they collectively pursued another strategy.
. This demonstrates the similarity between the Diner's dilemma and the Prisoner's dilemma. Like the Prisoner's dilemma, everyone is worse off by playing the unique equilibrium than they would have been if they collectively pursued another strategy.
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, the Unscrupulous diner's dilemma (or just Diner's dilemma) is an n-player
N-player game
In game theory, an n-player game is a game which is well defined for any number of players. This is usually used in contrast to standard 2-player games that are only specified for two players...
prisoner's dilemma
Prisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
. The situation imagined is that several individuals go out to eat, and prior to ordering they agree to split the check equally between all of them. Each individual must now choose whether to order the expensive or inexpensive dish. It is presupposed that the expensive dish is better than the cheaper, but not by enough to warrant paying the difference compared to eating alone. Each individual reasons that the expense they add to their bill by ordering the more expensive item is very small, and thus the improved dining experience is worth the money. However, every individual reasons this way and they all end up paying for the cost of the more expensive meal, which, by assumption, is worse for everyone than ordering and paying for the cheaper meal.
Formal definition and equilibrium analysis
Let g represent the joy of eating the expensive meal, b the joy of eating the cheap meal, h is the cost of the expensive meal, l the cost of the cheap meal, and n the number of players. From the description above we have the following ordering . Also, in order to make the game sufficiently similar to the Prisoner's dilemma
. Also, in order to make the game sufficiently similar to the Prisoner's dilemmaPrisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
we presume that one would prefer to order the expensive meal given others will help defray the cost,
Consider an arbitrary set of strategies by a player's opponent. Let the total cost of the other player's meals be x. The cost of ordering the cheap meal is
 and the cost of ordering the expensive meal is
and the cost of ordering the expensive meal is  . So the utilities for each meal are
. So the utilities for each meal are  for the expensive meal and
for the expensive meal and  for the cheaper meal. By assumption, the utility of ordering the expensive meal is higher. Remember that the choice of opponents' strategies was arbitrary and that the situation is symmetric. This proves that the expensive meal is strictly dominant
for the cheaper meal. By assumption, the utility of ordering the expensive meal is higher. Remember that the choice of opponents' strategies was arbitrary and that the situation is symmetric. This proves that the expensive meal is strictly dominantDominance (game theory)
In game theory, strategic dominance occurs when one strategy is better than another strategy for one player, no matter how that player's opponents may play...
and thus the unique Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
.
If everyone orders the expensive meal all of the diners pay h and their total utility is
 . On the other hand suppose that all the individuals had ordered the cheap meal, their utility would have been
. On the other hand suppose that all the individuals had ordered the cheap meal, their utility would have been  . This demonstrates the similarity between the Diner's dilemma and the Prisoner's dilemma. Like the Prisoner's dilemma, everyone is worse off by playing the unique equilibrium than they would have been if they collectively pursued another strategy.
. This demonstrates the similarity between the Diner's dilemma and the Prisoner's dilemma. Like the Prisoner's dilemma, everyone is worse off by playing the unique equilibrium than they would have been if they collectively pursued another strategy.
