
Erdős–Turán inequality
Encyclopedia
In mathematics, the Erdős–Turán inequality bounds the distance between a probability measure
on the circle and the Lebesgue measure
, in terms of Fourier coefficients. It was proved by Paul Erdős
and Paul Turán in 1948.
Let μ be a probability measure on the unit circle R/Z. The Erdős–Turán inequality states that, for any natural number n,
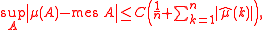
where the supremum is over all arcs
A ⊂ R/Z of the unit circle, mes stands for the Lebesgue measure,
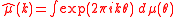
are the Fourier coefficients of μ, and C > 0 is a numerical constant.
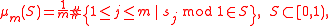
yields the following bound for the discrepancy:

This inequality holds for arbitrary natural numbers m,n, and gives a quantitative form of Weyl's criterion
for equidistribution.
A multi-dimensional variant of (1) is known as the Erdős–Turán–Koksma inequality.
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
on the circle and the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, in terms of Fourier coefficients. It was proved by Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and Paul Turán in 1948.
Let μ be a probability measure on the unit circle R/Z. The Erdős–Turán inequality states that, for any natural number n,
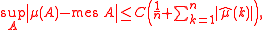
where the supremum is over all arcs
Arc (geometry)
In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...
A ⊂ R/Z of the unit circle, mes stands for the Lebesgue measure,
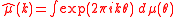
are the Fourier coefficients of μ, and C > 0 is a numerical constant.
Application to discrepancy
Let s1, s2, s3 ... ∈ R be a sequence. The Erdős–Turán inequality applied to the measure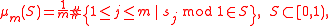
yields the following bound for the discrepancy:

This inequality holds for arbitrary natural numbers m,n, and gives a quantitative form of Weyl's criterion
Weyl's criterion
In mathematics, in the theory of diophantine approximation, Weyl's criterion states that a sequence of real numbers is equidistributed mod 1 if and only if for all non-zero integers \ell we have:...
for equidistribution.
A multi-dimensional variant of (1) is known as the Erdős–Turán–Koksma inequality.

