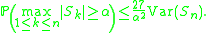Etemadi's inequality
Encyclopedia
In probability theory
, Etemadi's inequality is a so-called "maximal inequality", an inequality that gives a bound on the probability
that the partial sums of a finite collection of independent random variables exceed some specified bound. The result is due to Nasrollah Etemadi.
, and let α ≥ 0. Let Sk denote the partial sum
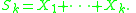
Then
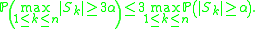
zero. Apply Chebyshev's inequality
to the right-hand side of Etemadi's inequality and replace α by α / 3. The result is Kolmogorov's inequality
with an extra factor of 27 on the right-hand side:
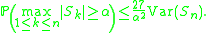
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Etemadi's inequality is a so-called "maximal inequality", an inequality that gives a bound on the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that the partial sums of a finite collection of independent random variables exceed some specified bound. The result is due to Nasrollah Etemadi.
Statement of the inequality
Let X1, ..., Xn be independent real-valued random variables defined on some common probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, and let α ≥ 0. Let Sk denote the partial sum
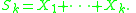
Then
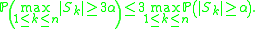
Remark
Suppose that the random variables Xk have common expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
zero. Apply Chebyshev's inequality
Chebyshev's inequality
In probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
to the right-hand side of Etemadi's inequality and replace α by α / 3. The result is Kolmogorov's inequality
Kolmogorov's inequality
In probability theory, Kolmogorov's inequality is a so-called "maximal inequality" that gives a bound on the probability that the partial sums of a finite collection of independent random variables exceed some specified bound...
with an extra factor of 27 on the right-hand side: