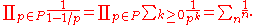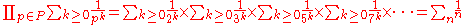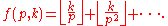Euclid's theorem
Encyclopedia
Euclid's theorem is a fundamental statement in number theory
that asserts that there are infinitely many prime number
s. There are several well-known proofs of the theorem
.
offered the following proof published in his work Elements
(Book IX, Proposition 20) and paraphrased here.
Take any finite list of prime numbers p1, p2, ..., pn. It will be shown that at least one additional prime number not in this list exists. Let P be the product of all the prime numbers in the list: P = p1p2...pn. Let q = P + 1. Then, q is either prime or not:
This proves that for any finite list of prime numbers, there is a prime number not on the list. Therefore there must be infinitely many prime numbers.
It is often erroneously reported that Euclid proved this result by contradiction, beginning with the assumption that the set initially considered contains all prime numbers, or that it contains precisely the n smallest primes, rather than any arbitrary finite set of primes. Although the proof as a whole is not by contradiction, in that it does not begin by assuming that only finitely many primes exist, there is a proof by contradiction within it: that is the proof that none of the initially considered primes can divide the number called q above.
, relies on the fundamental theorem of arithmetic
: that every integer has a unique prime factorization. If P is the set of all prime numbers, Euler wrote that:
The first equality is given by the formula for a geometric series in each term of the product. To show the second equality, distribute the product over the sum:
in the result, every product of primes appears exactly once, so by the fundamental theorem of arithmetic, the sum is equal to the sum over all integers.
The sum on the right is the harmonic series
, which diverges. So the product on the left must diverge also. Since each term of the product is finite, the number of terms must be infinite, so there is an infinite number of primes.
.
Let p1, ..., pN be the smallest N primes. Then by the inclusion–exclusion principle, the number of positive integers less than or equal to x that are divisible by one of those primes is
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
that asserts that there are infinitely many prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. There are several well-known proofs of the theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
.
Euclid's proof
EuclidEuclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
offered the following proof published in his work Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
(Book IX, Proposition 20) and paraphrased here.
Take any finite list of prime numbers p1, p2, ..., pn. It will be shown that at least one additional prime number not in this list exists. Let P be the product of all the prime numbers in the list: P = p1p2...pn. Let q = P + 1. Then, q is either prime or not:
- If q is prime then there is at least one more prime than is listed.
- If q is not prime then some prime factorPrime factorIn number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
p divides q. This factor p is not on our list: if it were, then it would divide P (since P is the product of every number on the list); but as we know, p divides P + 1 = q. Then p would have to divide the difference of the two numbers, which is (P + 1) − P or just 1. But no prime number divides 1 so there would be a contradiction, and therefore p cannot be on the list. This means at least one more prime number exists beyond those in the list.
This proves that for any finite list of prime numbers, there is a prime number not on the list. Therefore there must be infinitely many prime numbers.
It is often erroneously reported that Euclid proved this result by contradiction, beginning with the assumption that the set initially considered contains all prime numbers, or that it contains precisely the n smallest primes, rather than any arbitrary finite set of primes. Although the proof as a whole is not by contradiction, in that it does not begin by assuming that only finitely many primes exist, there is a proof by contradiction within it: that is the proof that none of the initially considered primes can divide the number called q above.
Euler's proof
Another proof, by the Swiss mathematician Leonhard EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, relies on the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
: that every integer has a unique prime factorization. If P is the set of all prime numbers, Euler wrote that:
The first equality is given by the formula for a geometric series in each term of the product. To show the second equality, distribute the product over the sum:
in the result, every product of primes appears exactly once, so by the fundamental theorem of arithmetic, the sum is equal to the sum over all integers.
The sum on the right is the harmonic series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
, which diverges. So the product on the left must diverge also. Since each term of the product is finite, the number of terms must be infinite, so there is an infinite number of primes.
Fürstenberg's proof
In the 1950s, Hillel Fürstenberg introduced a proof using point-set topology. See Fürstenberg's proof of the infinitude of primesFurstenberg's proof of the infinitude of primes
In number theory, Hillel Fürstenberg's proof of the infinitude of primes is a celebrated topological proof that the integers contain infinitely many prime numbers. When examined closely, the proof is less a statement about topology than a statement about certain properties of arithmetic sequences....
.
Pinasco
Juan Pablo Pinasco has written the following proof.Let p1, ..., pN be the smallest N primes. Then by the inclusion–exclusion principle, the number of positive integers less than or equal to x that are divisible by one of those primes is
-
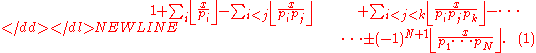
Dividing by x and letting x → ∞, we get
This can be written as
If no other primes than p1, ..., pN exist, then the expression in (1) is equal to and hence the expression in (2) is equal to 1. But clearly the expression in (3) is less than 1. Hence there must be more primes than p1, ..., pN.
and hence the expression in (2) is equal to 1. But clearly the expression in (3) is less than 1. Hence there must be more primes than p1, ..., pN.
Whang
Junho Peter Whang has recently published the following proof by contradiction. Let k be any positive integer. Then according to de Polignac's formulaDe Polignac's formulaIn number theory, de Polignac's formula, named after Alphonse de Polignac, gives the prime decomposition of the factorial n!, where n ≥ 1 is an integer. L. E. Dickson attributes the formula to Legendre.-The formula:...
(actually due to LegendreAdrien-Marie LegendreAdrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
)
where
Note that
But if only finitely many primes exist, then
so that is impossible.
Proof using Euler's totient function
The theorem can be also proved by using Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
φ. In this proof, the following property will be used:
Assume that there is only a finite number of primes. Call them p1, p2, ..., pr and consider the integer n = p1p2 ... pr. Any natural number a ≤ n has a prime divisor q. Then, q must be one of p1, p2, ..., pr, since that is the list of all prime numbers. Hence, for all a ≤ n, gcd(a, n) > 1 except if a = 1. This leads to φ(n) = 1, which contradicts the property above.
Proof using the irrationality of π
The following formula was discovered by EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
.

Each denominator is the multiple of four nearest to the numerator.
If there were finitely many primes, would be rational. This contradicts the fact that is irrational. However, to prove that is irrational is considerably more onerous than to prove that infinitely many primes exist.
External links
- Euclid's Elements, Book IX, Prop. 20 (Euclid's proof, on David Joyce's website at Clark University)
-