
Euler's criterion
Encyclopedia
In mathematics
, Euler's criterion is used in determining in number theory
whether a given integer
is a quadratic residue modulo
a prime
.
Let p be an odd prime and a an integer coprime
to p. Then
a is a quadratic residue modulo p (i.e. there exists a number k such that k2 ≡ a (mod p)) if and only if
As a corollary of the theorem one gets:
If a is not a square (also called a quadratic non-residue) modulo p then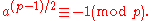
Euler's criterion can be concisely reformulated using the Legendre symbol
: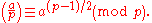
), a(p−1)/2 is either 1 or −1 (mod p). This immediately implies that the criterion are equivalent to the biimplication
:
We prove each direction separately.
(1) Assume a is a quadratic residue modulo p. We pick k such that k2 ≡ a (mod p). Then
The first step is valid since a ≡ b (mod n) implies am ≡ bm(mod n) (see modular arithmetic#Congruence relation), while the second step is Fermat's little theorem again.
(2) Assume a(p − 1)/2 ≡ 1 (mod p). Then let α be a primitive root
modulo p, so that a can be written as αi for some i. In particular, αi(p−1)/2 ≡ 1 (mod p). Since α is a primitive root, its multiplicative order
is p − 1, so p − 1 must divide
i(p − 1)/2, so i must be even. Let k ≡ αi/2 (mod p). We finally have k2 = αi ≡ a (mod p).
Let a = 17. For which primes p is 17 a quadratic residue?
We can test prime ps manually given the formula above.
In one case, testing p = 3, we have 17(3 − 1)/2 = 171 ≡ 2 ≡ −1 (mod 3), therefore 17 is not a quadratic residue modulo 3.
In another case, testing p = 13, we have 17(13 − 1)/2 = 176 ≡ 1 (mod 13), therefore 17 is a quadratic residue modulo 13. As confirmation, note that 17 ≡ 4 (mod 13), and 22 = 4.
We can do these calculations faster by using various modular arithmetic and Legendre symbol properties.
If we keep calculating the values, we find: = +1 for p = {13, 19, ...} (17 is a quadratic residue modulo these values)
= −1 for p = {3, 5, 7, 11, 23, ...} (17 is not a quadratic residue modulo these values).
Example 2: Finding residues given a prime modulus p
Which numbers are squares modulo 17 (quadratic residues modulo 17)?
We can manually calculate:
So the set of the quadratic residues modulo 17 is {1,2,4,8,9,13,15,16}. Note that we did not need to calculate squares for the values 9 through 16, as they are all negatives of the previously squared values (e.g. 9 ≡ −8 (mod 17), so 92 ≡ (−8)2 = 64 ≡ 13 (mod 17)).
We can find quadratic residues or verify them using the above formula. To test if 2 is a quadratic residue modulo 17, we calculate 2(17 − 1)/2 = 28 ≡ 1 (mod 17), so it is a quadratic residue. To test if 3 is a quadratic residue modulo 17, we calculate 3(17 − 1)/2 = 38 ≡ 16 ≡ −1 (mod 17), so it is not a quadratic residue.
Euler's criterion is related to the Law of quadratic reciprocity
and is used in a definition of Euler–Jacobi pseudoprimes.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Euler's criterion is used in determining in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
whether a given integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
is a quadratic residue modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
a prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
.
Definition
Euler's criterion states:Let p be an odd prime and a an integer coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to p. Then
a is a quadratic residue modulo p (i.e. there exists a number k such that k2 ≡ a (mod p)) if and only if

As a corollary of the theorem one gets:
If a is not a square (also called a quadratic non-residue) modulo p then
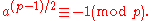
Euler's criterion can be concisely reformulated using the Legendre symbol
Legendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
:
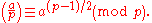
Proof of Euler's criterion
Every number either is or isn't a quadratic residue (mod p). Also, since the square-roots of 1 are 1 and −1 (mod p), and since ap−1 ≡ 1 (mod p) (Fermat's little theoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
), a(p−1)/2 is either 1 or −1 (mod p). This immediately implies that the criterion are equivalent to the biimplication
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
:
- a is a quadratic residue modulo p if and only if a(p−1)/2 ≡ 1 (mod p).
We prove each direction separately.
(1) Assume a is a quadratic residue modulo p. We pick k such that k2 ≡ a (mod p). Then
- a(p−1)/2 ≡ kp−1 ≡ 1 (mod p).
The first step is valid since a ≡ b (mod n) implies am ≡ bm(mod n) (see modular arithmetic#Congruence relation), while the second step is Fermat's little theorem again.
(2) Assume a(p − 1)/2 ≡ 1 (mod p). Then let α be a primitive root
Primitive root modulo n
In modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
modulo p, so that a can be written as αi for some i. In particular, αi(p−1)/2 ≡ 1 (mod p). Since α is a primitive root, its multiplicative order
Multiplicative order
In number theory, given an integer a and a positive integer n with gcd = 1, the multiplicative order of a modulo n is the smallest positive integer k withThe order of a modulo n is usually written ordn, or On.- Example :To determine the multiplicative order of 4 modulo 7, we compute 42 = 16 ≡ 2 ...
is p − 1, so p − 1 must divide
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
i(p − 1)/2, so i must be even. Let k ≡ αi/2 (mod p). We finally have k2 = αi ≡ a (mod p).
Examples
Example 1: Finding primes for which a is a residueLet a = 17. For which primes p is 17 a quadratic residue?
We can test prime ps manually given the formula above.
In one case, testing p = 3, we have 17(3 − 1)/2 = 171 ≡ 2 ≡ −1 (mod 3), therefore 17 is not a quadratic residue modulo 3.
In another case, testing p = 13, we have 17(13 − 1)/2 = 176 ≡ 1 (mod 13), therefore 17 is a quadratic residue modulo 13. As confirmation, note that 17 ≡ 4 (mod 13), and 22 = 4.
We can do these calculations faster by using various modular arithmetic and Legendre symbol properties.
If we keep calculating the values, we find: = +1 for p = {13, 19, ...} (17 is a quadratic residue modulo these values)
= −1 for p = {3, 5, 7, 11, 23, ...} (17 is not a quadratic residue modulo these values).
Example 2: Finding residues given a prime modulus p
Which numbers are squares modulo 17 (quadratic residues modulo 17)?
We can manually calculate:
- 12 = 1
- 22 = 4
- 32 = 9
- 42 = 16
- 52 = 25 ≡ 8 (mod 17)
- 62 = 36 ≡ 2 (mod 17)
- 72 = 49 ≡ 15 (mod 17)
- 82 = 64 ≡ 13 (mod 17).
So the set of the quadratic residues modulo 17 is {1,2,4,8,9,13,15,16}. Note that we did not need to calculate squares for the values 9 through 16, as they are all negatives of the previously squared values (e.g. 9 ≡ −8 (mod 17), so 92 ≡ (−8)2 = 64 ≡ 13 (mod 17)).
We can find quadratic residues or verify them using the above formula. To test if 2 is a quadratic residue modulo 17, we calculate 2(17 − 1)/2 = 28 ≡ 1 (mod 17), so it is a quadratic residue. To test if 3 is a quadratic residue modulo 17, we calculate 3(17 − 1)/2 = 38 ≡ 16 ≡ −1 (mod 17), so it is not a quadratic residue.
Euler's criterion is related to the Law of quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
and is used in a definition of Euler–Jacobi pseudoprimes.

