
Euler's theorem
Encyclopedia
In number theory
, Euler's theorem (also known as the Fermat–Euler theorem or Euler's totient theorem) states that if n and a are coprime
positive integers, then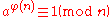
where φ(n) is Euler's totient function
and "... ≡ ... (mod n)" denotes congruence modulo n
.
The converse of Euler's theorem is also true: if the above congruence holds for positive integers a and n, then a and n are coprime.
The theorem is a generalization of Fermat's little theorem
, and is further generalized by Carmichael's theorem.
The theorem may be used to easily reduce large powers modulo n. For example, consider finding the ones place decimal digit of 7222, i.e. 7222 (mod 10). Note that 7 and 10 are coprime, and φ(10) = 4. So Euler's theorem yields 74 ≡ 1 (mod 10), and we get 7222 ≡ 74×55 + 2 ≡ (74)55×72 ≡ 155×72 ≡ 49 ≡ 9 (mod 10).
In general, when reducing a power of a modulo n (where a and n are coprime), one needs to work modulo φ(n) in the exponent of a:
Euler's theorem also forms the basis of the RSA encryption system: encryption and decryption in this system together amount to exponentiating the original text by kφ(n)+1 for some positive integer k, so Euler's theorem shows that the decrypted result is the same as the original.
published a proof in 1789. Using modern terminology, one may prove the theorem as follows: the numbers a which are relatively prime to n form a group
under multiplication mod n, the group G of (multiplicative) units of the ring Z/nZ. This group has φ(n) elements. The element a := a (mod n) is a member of the group G, and the order o(a) of a (the least k > 0 such that ak = 1) must have a multiple equal to the size of G. (The order of a is the size of the subgroup of G generated by a, and Lagrange's theorem
states that the size of any subgroup of G divides the size of G.)
Thus for some integer M > 0, M·o(a) = φ(n). Therefore aφ(n) = ao(a)·M = (ao(a))M = 1M = 1. This means that aφ(n) = 1 (mod n).
2. Another direct proof: if a is coprime to n, then multiplication by a
permutes the residue classes mod n that are coprime
to n; in other words (writing R for
the set consisting of the φ(n) different such classes) the sets
{ x : x in R } and
{ ax : x in R } are equal; therefore,
the two products over all of the elements in each set are equal. Hence, P ≡ aφ(n)P (mod n) where P is the product over all of the elements in the first set. Since P is coprime to n, it follows that aφ(n) ≡ 1 (mod n).
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Euler's theorem (also known as the Fermat–Euler theorem or Euler's totient theorem) states that if n and a are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
positive integers, then
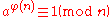
where φ(n) is Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
and "... ≡ ... (mod n)" denotes congruence modulo n
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
.
The converse of Euler's theorem is also true: if the above congruence holds for positive integers a and n, then a and n are coprime.
The theorem is a generalization of Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
, and is further generalized by Carmichael's theorem.
The theorem may be used to easily reduce large powers modulo n. For example, consider finding the ones place decimal digit of 7222, i.e. 7222 (mod 10). Note that 7 and 10 are coprime, and φ(10) = 4. So Euler's theorem yields 74 ≡ 1 (mod 10), and we get 7222 ≡ 74×55 + 2 ≡ (74)55×72 ≡ 155×72 ≡ 49 ≡ 9 (mod 10).
In general, when reducing a power of a modulo n (where a and n are coprime), one needs to work modulo φ(n) in the exponent of a:
- if x ≡ y (mod φ(n)), then ax ≡ ay (mod n).
Euler's theorem also forms the basis of the RSA encryption system: encryption and decryption in this system together amount to exponentiating the original text by kφ(n)+1 for some positive integer k, so Euler's theorem shows that the decrypted result is the same as the original.
Proofs
1. Leonhard EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
published a proof in 1789. Using modern terminology, one may prove the theorem as follows: the numbers a which are relatively prime to n form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under multiplication mod n, the group G of (multiplicative) units of the ring Z/nZ. This group has φ(n) elements. The element a := a (mod n) is a member of the group G, and the order o(a) of a (the least k > 0 such that ak = 1) must have a multiple equal to the size of G. (The order of a is the size of the subgroup of G generated by a, and Lagrange's theorem
Lagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
states that the size of any subgroup of G divides the size of G.)
Thus for some integer M > 0, M·o(a) = φ(n). Therefore aφ(n) = ao(a)·M = (ao(a))M = 1M = 1. This means that aφ(n) = 1 (mod n).
2. Another direct proof: if a is coprime to n, then multiplication by a
permutes the residue classes mod n that are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to n; in other words (writing R for
the set consisting of the φ(n) different such classes) the sets
{ x : x in R } and
{ ax : x in R } are equal; therefore,
the two products over all of the elements in each set are equal. Hence, P ≡ aφ(n)P (mod n) where P is the product over all of the elements in the first set. Since P is coprime to n, it follows that aφ(n) ≡ 1 (mod n).

