Ewald's sphere
Encyclopedia
The Ewald sphere is a geometric construct used in electron
, neutron
, and X-ray crystallography
which demonstrates the relationship between:
It was conceived by Paul Peter Ewald
, a German physicist and crystallographer. Ewald himself spoke of the sphere of reflection.
Ewald's sphere can be used to find the maximum resolution
available for a given x-ray wavelength and the unit cell dimensions. It is often simplified to the two-dimensional "Ewald's circle" model or may be referred to as the Ewald sphere.
can be described as a lattice
of points of equal symmetry. The requirement for constructive interference in a diffraction experiment means that in momentum or reciprocal space the values of momentum transfer where constructive interference occurs also form a lattice (the reciprocal lattice
). For example, the reciprocal lattice of a simple cubic
real-space lattice is also a simple cubic structure. The aim of the Ewald sphere is to determine which lattice planes (represented by the grid points on the reciprocal lattice) will result in a diffracted signal for a given wavelength,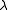
, of incident radiation.
The incident plane wave falling on the crystal has a wave vector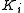
whose length is 
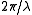. The diffracted plane wave has a wave vector 
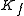. If no energy is gained or lost in the diffraction process (it is elastic) then 
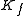has the same length as 
. The difference between the wave-vectors of diffracted and incident wave is defined as scattering vector 
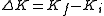. Since 
and 
have the same length the scattering vector must lie on the surface of a sphere of radius 
. This sphere is called the Ewald sphere.
The reciprocal lattice points are the values of momentum transfer where the Bragg diffraction condition is satisfied and for diffraction to occur the scattering vector must be equal to a reciprocal lattice vector. Geometrically this means that if the origin of reciprocal space is placed at the tip of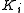
then diffraction will occur only for reciprocal lattice points that lie on the surface of the Ewald sphere.
. In this approximation, diffraction patterns in effect illuminate planar slices through the origin of a crystal's reciprocal lattice
. However, it is important to note that while the Ewald sphere may be quite flat, a diffraction pattern taken perfectly aligned down a zone axis (high-symmetry direction) contains precisely zero spots that exactly satisfy the Bragg condition. As one tilts a single crystal with respect to the incident beam, diffraction spots wink on and off as the Ewald sphere cuts through one zero order Laue zone (ZOLZ) after another.
Electron crystallography
Electron crystallography is a method to determine the arrangement of atoms in solids using a transmission electron microscope .- Comparison with X-ray crystallography :...
, neutron
Neutron diffraction
Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material: A sample to be examined is placed in a beam of thermal or cold neutrons to obtain a diffraction pattern that provides information of...
, and X-ray crystallography
X-ray crystallography
X-ray crystallography is a method of determining the arrangement of atoms within a crystal, in which a beam of X-rays strikes a crystal and causes the beam of light to spread into many specific directions. From the angles and intensities of these diffracted beams, a crystallographer can produce a...
which demonstrates the relationship between:
- the wavevector of the incident and diffracted x-ray beams,
- the diffraction angle for a given reflection,
- the reciprocal latticeReciprocal latticeIn physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
of the crystalCrystalA crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
It was conceived by Paul Peter Ewald
Paul Peter Ewald
Paul Peter Ewald was a German-born U.S. crystallographer and physicist, a pioneer of X-ray diffraction methods.-Education:...
, a German physicist and crystallographer. Ewald himself spoke of the sphere of reflection.
Ewald's sphere can be used to find the maximum resolution
Resolution (electron density)
Resolution in terms of electron density is a measure of the resolvability in the electron density map of a molecule. In X-ray crystallography, resolution is the highest resolvable peak in the diffraction pattern...
available for a given x-ray wavelength and the unit cell dimensions. It is often simplified to the two-dimensional "Ewald's circle" model or may be referred to as the Ewald sphere.
Ewald Construction
A crystalCrystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
can be described as a lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
of points of equal symmetry. The requirement for constructive interference in a diffraction experiment means that in momentum or reciprocal space the values of momentum transfer where constructive interference occurs also form a lattice (the reciprocal lattice
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
). For example, the reciprocal lattice of a simple cubic
Cubic crystal system
In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals....
real-space lattice is also a simple cubic structure. The aim of the Ewald sphere is to determine which lattice planes (represented by the grid points on the reciprocal lattice) will result in a diffracted signal for a given wavelength,
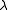, of incident radiation.The incident plane wave falling on the crystal has a wave vector
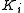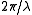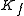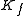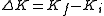whose length is . The diffracted plane wave has a wave vector . If no energy is gained or lost in the diffraction process (it is elastic) then has the same length as . The difference between the wave-vectors of diffracted and incident wave is defined as scattering vector . Since and have the same length the scattering vector must lie on the surface of a sphere of radius . This sphere is called the Ewald sphere.The reciprocal lattice points are the values of momentum transfer where the Bragg diffraction condition is satisfied and for diffraction to occur the scattering vector must be equal to a reciprocal lattice vector. Geometrically this means that if the origin of reciprocal space is placed at the tip of
then diffraction will occur only for reciprocal lattice points that lie on the surface of the Ewald sphere.Small scattering-angle limit
When the wavelength of the radiation to be scattered is much smaller than the spacing between atoms, the Ewald sphere radius becomes large compared to the spatial frequency of atomic planes. This is common, for example, in transmission electron microscopyTransmission electron microscopy
Transmission electron microscopy is a microscopy technique whereby a beam of electrons is transmitted through an ultra thin specimen, interacting with the specimen as it passes through...
. In this approximation, diffraction patterns in effect illuminate planar slices through the origin of a crystal's reciprocal lattice
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
. However, it is important to note that while the Ewald sphere may be quite flat, a diffraction pattern taken perfectly aligned down a zone axis (high-symmetry direction) contains precisely zero spots that exactly satisfy the Bragg condition. As one tilts a single crystal with respect to the incident beam, diffraction spots wink on and off as the Ewald sphere cuts through one zero order Laue zone (ZOLZ) after another.