
Fermat's spiral
Encyclopedia


in polar coordinates (the more general Fermat's spiral follows r 2 = a 2θ.)
It is a type of Archimedean spiral.
In disc phyllotaxis
Phyllotaxis
In botany, phyllotaxis or phyllotaxy is the arrangement of leaves on a plant stem .- Pattern structure :...
(sunflower
Sunflower
Sunflower is an annual plant native to the Americas. It possesses a large inflorescence . The sunflower got its name from its huge, fiery blooms, whose shape and image is often used to depict the sun. The sunflower has a rough, hairy stem, broad, coarsely toothed, rough leaves and circular heads...
, daisy), the mesh of spirals occurs in Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s because divergence (angle of succession in a single spiral arrangement) approaches the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
. The shape of the spirals depends on the growth of the elements generated sequentially. In mature-disc phyllotaxis
Phyllotaxis
In botany, phyllotaxis or phyllotaxy is the arrangement of leaves on a plant stem .- Pattern structure :...
, when all the elements are the same size, the shape of the spirals is that of Fermat spirals—ideally. That is because Fermat's spiral traverses equal annuli
Annulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
in equal turns. The full model proposed by H Vogel in 1979 is

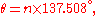
where θ is the angle, r is the radius or distance from the center, and n is the index number of the floret and c is a constant scaling factor. The angle 137.508° is the golden angle
Golden angle
In geometry, the golden angle is the smaller of the two angles created by sectioning the circumference of a circle according to the golden section; that is, into two arcs such that the ratio of the length of the larger arc to the length of the smaller arc is the same as the ratio of the full...
which is approximated by ratios of Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s.

