
Fortune's algorithm
Encyclopedia

Sweep line algorithm
In computational geometry, a sweep line algorithm or plane sweep algorithm is a type of algorithm that uses a conceptual sweep line or sweep surface to solve various problems in Euclidean space...
for generating a Voronoi diagram
Voronoi diagram
In mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
from a set of points in a plane using O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n log n) time and O(n) space. It was originally published by Steven Fortune in 1986 in his paper "A sweepline algorithm for Voronoi diagrams."
Algorithm description
The algorithm maintains both a sweep line and a beach line, which both move through the plane as the algorithm progresses. The sweep line is a straight line, which we may by convention assume to be vertical and moving left to right across the plane. At any time during the algorithm, the input points left of the sweep line will have been incorporated into the Voronoi diagram, while the points right of the sweep line will not have been considered yet. The beach line is not a line, but a complex curve to the left of the sweep line, composed of pieces of parabolaParabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
s; it divides the portion of the plane within which the Voronoi diagram can be known, regardless of what other points might be right of the sweep line, from the rest of the plane. For each point left of the sweep line, one can define a parabola of points equidistant from that point and from the sweep line; the beach line is the boundary of the union of these parabolas. As the sweep line progresses, the vertices of the beach line, at which two parabolas cross, trace out the edges of the Voronoi diagram.
The algorithm maintains as data structures a binary search tree
Binary search tree
In computer science, a binary search tree , which may sometimes also be called an ordered or sorted binary tree, is a node-based binary tree data structurewhich has the following properties:...
describing the combinatorial structure of the beach line, and a priority queue
Priority queue
A priority queue is an abstract data type in computer programming.It is exactly like a regular queue or stack data structure, but additionally, each element is associated with a "priority"....
listing potential future events that could change the beach line structure. These events include the addition of another parabola to the beach line (when the sweep line crosses another input point) and the removal of a curve from the beach line (when the sweep line becomes tangent to a circle through some three input points whose parabolas form consecutive segments of the beach line). Each such event may be prioritized by the x-coordinate of the sweep line at the point the event occurs. The algorithm itself then consists of repeatedly removing the next event from the priority queue, finding the changes the event causes in the beach line, and updating the data structures. As there are O(n) events to process (each being associated with some feature of the Voronoi diagram) and O(log n) time to process an event (each consisting of a constant number of binary search tree and priority queue operations) the total time is O(n log n).
Pseudocode
PseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
description of algorithm
Note: This pseudocode uses a horizontal sweepline and not vertical as in the above example.
let
 be the transformation
be the transformation  , where
, where 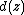 is a parabola with minimum at
is a parabola with minimum at 
let T be the "beach line"
let
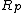 be the region covered by site p.
be the region covered by site p.let
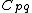 be the boundary ray between sites
be the boundary ray between sites 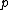 and
and 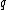 .
.let
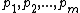 be the sites with minimal
be the sites with minimal 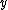 -coordinate, ordered by
-coordinate, ordered by  -coordinate
-coordinate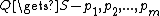
create initial vertical boundary rays

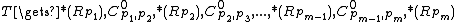
while not IsEmpty(
 ) do
) do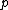 ← DeleteMin(
← DeleteMin(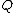 )
)case
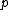 of
of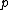 is a site in
is a site in  :
:find the occurrence of a region
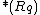 in
in 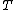 containing
containing  ,
,bracketed by
 on the left and
on the left and 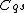 on the right
on the rightcreate new boundary rays
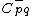 and
and 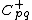 with bases
with bases 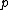
replace
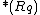 with
with 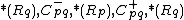 in
in 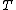
delete from
 any intersection between
any intersection between  and
and 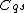
insert into
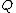 any intersection between
any intersection between  and
and 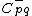
insert into
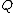 any intersection between
any intersection between 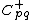 and
and 
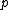 is a Voronoi vertex in
is a Voronoi vertex in 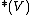 :
:let
 be the intersection of
be the intersection of 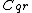 on the left and
on the left and 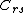 on the right
on the rightlet
 be the left neighbor of
be the left neighbor of  and
andlet
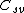 be the right neighbor of
be the right neighbor of 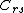 in
in 
create a new boundary ray
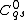 if
if 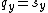 ,
,or create
 if
if 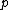 is right of the higher of
is right of the higher of 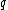 and
and  ,
,otherwise create
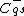
replace
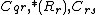 with newly created
with newly created 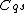 in
in 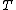
delete from
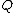 any intersection between
any intersection between 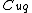 and
and 
delete from
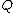 any intersection between
any intersection between 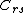 and
and 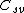
insert into
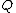 any intersection between
any intersection between 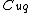 and
and 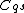
insert into
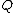 any intersection between
any intersection between 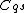 and
and 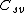
record
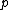 as the summit of
as the summit of  and
and 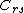 and the base of
and the base of 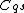
output the boundary segments
 and
and 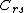
endcase
endwhile
output the remaining boundary rays in
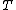
Weighted sites and disks
As Fortune describes in a modified version of the sweepline algorithm can be used to construct an additively weighted Voronoi diagram, in which the distance to each site is offset by the weight of the site; this may equivalently be viewed as a Voronoi diagram of a set of disks, centered at the sites with radius equal to the weight of the site.Weighted sites may be used to control the areas of the Voronoi cells when using Voronoi diagrams to construct treemaps. In an additively weighted Voronoi diagram, the bisector between sites is in general a hyperbola, in contrast to unweighted Voronoi diagrams and power diagrams of disks for which it is a straight line.

