Freivald's algorithm
Encyclopedia
Freivalds' algorithm is a randomized algorithm
used to verify matrix multiplication
. Given three n × n matrices
A, B, and C, a general problem is to verify whether A × B = C. A naïve algorithm
would compute the product A × B explicitly and compare term by term whether this product equals C. However, this approach takes O
(n3) time. To resolve this, Freivalds' algorithm utilizes randomization
in order to reduce this time bound to O
(n2).
A, B, C.
of error. We claim that if A × B = C, then p = 0, and if A × B ≠ C, then p ≤ 1/2.
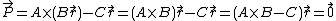, regardless of what our vector 
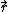was.
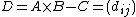, so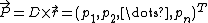 
.
Since A × B ≠ C, we have A × B − C ≠ 0, so some element of D is nonzero.
Suppose that the element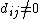
.
By the definition of matrix multiplication
, we have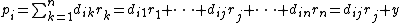
.
Using Bayes' Theorem
, we have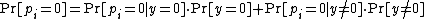
.
Also, note that: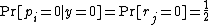
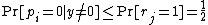
Plugging these in the above equation, we have:
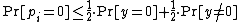
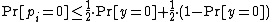
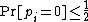
Therefore,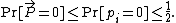
This completes the proof.
is O
(n2), beating the classical deterministic algorithm's
bound of O
(n3). The error analysis also shows that if we run our algorithm
k times, we can achieve an error bound of less than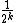
, an exponentially small quantity. Therefore, utilization of randomized algorithms can speed up a very slow deterministic algorithm
. In fact, the best known deterministic matrix multiplication verification algorithm known at the current time is the Coppersmith-Winograd algorithm with an asymptotic running time of O
(n2.376).
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
used to verify matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. Given three n × n matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A, B, and C, a general problem is to verify whether A × B = C. A naïve algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
would compute the product A × B explicitly and compare term by term whether this product equals C. However, this approach takes O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n3) time. To resolve this, Freivalds' algorithm utilizes randomization
Randomization
Randomization is the process of making something random; this means:* Generating a random permutation of a sequence .* Selecting a random sample of a population ....
in order to reduce this time bound to O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n2).
Input
Three n × n matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A, B, C.
Procedure
- Generate an n × 1 random 0/1 vector
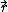. - Compute
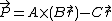. - Output "Yes" if
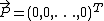; "No," otherwise.
Error analysis
Let p equal the probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of error. We claim that if A × B = C, then p = 0, and if A × B ≠ C, then p ≤ 1/2.
A × B = C
If A × B = C, then A × B − C = 0, and so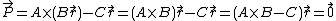, regardless of what our vector 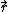was.A × B ≠ C
Let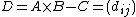, so 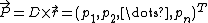.Since A × B ≠ C, we have A × B − C ≠ 0, so some element of D is nonzero.
Suppose that the element
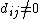.By the definition of matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, we have
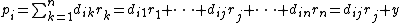.Using Bayes' Theorem
Bayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
, we have
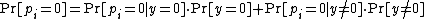.Also, note that:
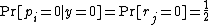
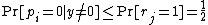
Plugging these in the above equation, we have:
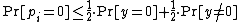
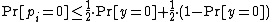
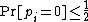
Therefore,
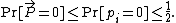
This completes the proof.
Ramifications
Simple algorithmic analysis shows that the running time of this algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n2), beating the classical deterministic algorithm's
Deterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
bound of O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n3). The error analysis also shows that if we run our algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
k times, we can achieve an error bound of less than
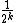, an exponentially small quantity. Therefore, utilization of randomized algorithms can speed up a very slow deterministic algorithmDeterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
. In fact, the best known deterministic matrix multiplication verification algorithm known at the current time is the Coppersmith-Winograd algorithm with an asymptotic running time of O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n2.376).