Fubini's theorem on differentiation
Encyclopedia
In mathematics, Fubini's theorem on differentiation, named after Guido Fubini
, is a result in real analysis
concerning the differentiation
of series of monotonic function
s. It can be proven by using Fatou's lemma
and the properties of null set
s.
is an interval
and that for every natural number
k,
is an increasing function. If,
exists for all
then,
almost everywhere
in I.
In general, if we don't suppose fk is increasing for every k, in order to get the same conclusion, we need a stricter condition like uniform convergence of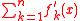
on I for every n.
Guido Fubini
Guido Fubini was an Italian mathematician, known for Fubini's theorem and the Fubini–Study metric.Born in Venice, he was steered towards mathematics at an early age by his teachers and his father, who was himself a teacher of mathematics...
, is a result in real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
concerning the differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of series of monotonic function
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
s. It can be proven by using Fatou's lemma
Fatou's lemma
In mathematics, Fatou's lemma establishes an inequality relating the integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions...
and the properties of null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
s.
Statement
Assume is an intervalInterval
Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
and that for every natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
k,
is an increasing function. If,exists for all
then,almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
in I.
In general, if we don't suppose fk is increasing for every k, in order to get the same conclusion, we need a stricter condition like uniform convergence of
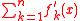on I for every n.