In mathematics, Gabriel's theorem, proved by Pierre Gabriel

Pierre Gabriel

Pierre Gabriel is a mathematician at Universität Zürich who works on category theory, algebraic groups, and representation theory of algebras. He was elected a correspondent member of the French Academy of Sciences in November 1986.-See also:...

, classifies the quivers

Quiver (mathematics)

In mathematics, a quiver is a directed graph where loops and multiple arrows between two vertices are allowed, i.e. a multidigraph. They are commonly used in representation theory: a representation, V, of a quiver assigns a vector space V to each vertex x of the quiver and a linear map V to each...

 of finite type in terms of Dynkin diagrams.

Statement

A quiver is of finite type if it has only finitely many isomorphism classes of indecomposable representations. classified all quivers of finite type, and also their indecomposable representations. More precisely, Gabriel's theorem states that:

1. A (connected) quiver is of finite type if and only if its underlying graph (when the directions of the arrows are ignored) is one of the ADE
   ADE classification
   In mathematics, the ADE classification is the complete list of simply laced Dynkin diagrams or other mathematical objects satisfying analogous axioms; "simply laced" means that there are no multiple edges, which corresponds to all simple roots in the root system forming angles of \pi/2 = 90^\circ ...
   
    Dynkin diagrams: , , , , .
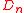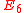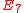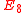2. The indecomposable representations are in a one-to-one correspondence with the positive roots of the root system
   Root system
   In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
   
   of the Dynkin diagram.

found a generalization of Gabriel's theorem in which all Dynkin diagrams of finite dimensional semisimple Lie algebras occur.