Gauss' principle of least constraint
Encyclopedia
The principle of least constraint is another formulation of classical mechanics
enunciated by Carl Friedrich Gauss
in 1829.
The principle of least constraint is a least squares
principle stating that the true motion of a mechanical system of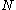
masses is the minimum of the quantity
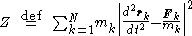
for all trajectories satisfying any imposed constraints, where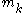
, 
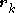and 
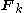represent the mass, position and applied forces of the 
mass.
Gauss' principle is equivalent to D'Alembert's principle
.
The principle of least constraint is qualitatively similar to Hamilton's principle
, which states that the true path taken by a mechanical system is an extremum of the action
. However, Gauss' principle is a true (local) minimal principle, whereas the other is an extremal principle.
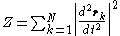
The kinetic energy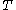
is also conserved under these conditions
Since the line element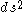
in the 
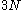-dimensional space of the coordinates is defined
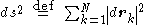
the conservation of energy may also be written
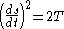
Dividing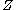
by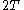 
yields another minimal quantity
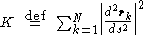
Since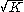
is the local curvature
of the trajectory in the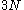
-dimensional space of the coordinates, minimization of 
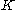is equivalent to finding the trajectory of least curvature (a geodesic
) that is consistent with the constraints. Hertz's principle is also a special case of Jacobi
's formulation of the least-action principle
.
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
enunciated by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in 1829.
The principle of least constraint is a least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
principle stating that the true motion of a mechanical system of
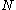masses is the minimum of the quantity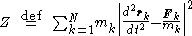for all trajectories satisfying any imposed constraints, where
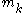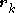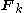, and represent the mass, position and applied forces of the mass.Gauss' principle is equivalent to D'Alembert's principle
D'Alembert's principle
D'Alembert's principle, also known as the Lagrange–d'Alembert principle, is a statement of the fundamental classical laws of motion. It is named after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert...
.
The principle of least constraint is qualitatively similar to Hamilton's principle
Hamilton's principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
, which states that the true path taken by a mechanical system is an extremum of the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
. However, Gauss' principle is a true (local) minimal principle, whereas the other is an extremal principle.
Hertz's principle of least curvature
Hertz's principle of least curvature is a special case of Gauss' principle, restricted by the two conditions that there be no applied forces and that all masses are identical. (Without loss of generality, the masses may be set equal to one.) Under these conditions, Gauss' minimized quantity can be written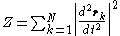The kinetic energy
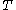is also conserved under these conditionsSince the line element
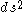in the 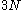-dimensional space of the coordinates is defined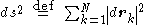the conservation of energy may also be written
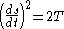
Dividing
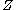by 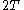yields another minimal quantity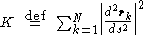Since
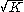is the local curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of the trajectory in the
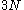-dimensional space of the coordinates, minimization of 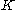is equivalent to finding the trajectory of least curvature (a geodesicGeodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
) that is consistent with the constraints. Hertz's principle is also a special case of Jacobi
Carl Gustav Jakob Jacobi
Carl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
's formulation of the least-action principle
Maupertuis' principle
In classical mechanics, Maupertuis' principle is an integral equation that determines the path followed by a physical system without specifying the time parameterization of that path. It is a special case of the more generally stated principle of least action...
.
External links
- http://eom.springer.de/g/g043500.htm Gauss' principle of least constraint
- http://eom.springer.de/H/h047140.htm Hertz's principle of least curvature