Gilbreath's conjecture
Encyclopedia
Gilbreath's conjecture is a hypothesis, or a conjecture, in number theory
regarding the sequence
s generated by applying the forward difference operator to consecutive prime numbers and leaving the results unsigned, and then repeating this process on consecutive terms in the resulting sequence, and so forth. The statement is named after mathematician Norman L. Gilbreath who, in 1958, presented it to the mathematical community after observing the pattern by chance while doing arithmetic on a napkin. In 1878, eighty years before Gilbreath's discovery, François Proth
had, however, published the same observations along with an attempted proof, which was later shown to be false.
Computing the absolute value
of the difference between term n+1 and term n in this sequence yields the sequence
If the same calculation is done for the terms in this new sequence, and the sequence that is the outcome of this process, and again ad infinitum for each sequence that is the output of such a calculation, the first five sequences in this list are given by
What Gilbreath—and François Proth before him—noticed is that the first term in each series of differences appears to be 1.
denote the ordered sequence of prime numbers 
, and define each term in the sequence 
by
,
where
is positive. Also, for each integer 
greater than 1, let the terms in 
be given by
.
Gilbreath's conjecture states that every term in the sequence
for positive 
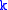is 1.
verified that
is 1 for 
in 1993, but the conjecture remains an open problem.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
regarding the sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s generated by applying the forward difference operator to consecutive prime numbers and leaving the results unsigned, and then repeating this process on consecutive terms in the resulting sequence, and so forth. The statement is named after mathematician Norman L. Gilbreath who, in 1958, presented it to the mathematical community after observing the pattern by chance while doing arithmetic on a napkin. In 1878, eighty years before Gilbreath's discovery, François Proth
François Proth
François Proth was a French self-taught mathematician farmer who lived in Vaux-devant-Damloup near Verdun, France. He stated four primality-related theorems, the most famous of which is Proth's theorem, published around 1878...
had, however, published the same observations along with an attempted proof, which was later shown to be false.
Motivating arithmetic
Gilbreath observed a pattern while playing with the ordered sequence of prime numbers- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ...
Computing the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the difference between term n+1 and term n in this sequence yields the sequence
- 1, 2, 2, 4, 2, 4, 2, 4, 6, 2, ...
If the same calculation is done for the terms in this new sequence, and the sequence that is the outcome of this process, and again ad infinitum for each sequence that is the output of such a calculation, the first five sequences in this list are given by
- 1, 0, 2, 2, 2, 2, 2, 2, 4, ...
- 1, 2, 0, 0, 0, 0, 0, 2, ...
- 1, 2, 0, 0, 0, 0, 2, ...
- 1, 2, 0, 0, 0, 2, ...
- 1, 2, 0, 0, 2, ...
What Gilbreath—and François Proth before him—noticed is that the first term in each series of differences appears to be 1.
The conjecture
Stating Gilbreath's observation formally is significantly easier to do after devising a notation for the sequences in the previous section. Toward this end, let denote the ordered sequence of prime numbers , and define each term in the sequence by,where
is positive. Also, for each integer greater than 1, let the terms in be given by.Gilbreath's conjecture states that every term in the sequence
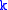for positive is 1.Verification and attempted proofs
, no valid proof of the conjecture has been published. As mentioned in the introduction, François Proth released what he believed to be a proof of the statement that was later shown to be flawed. Andrew OdlyzkoAndrew Odlyzko
Andrew Michael Odlyzko is a mathematician and a former head of the University of Minnesota's Digital Technology Center.In the field of mathematics he has published extensively on analytic number theory, computational number theory, cryptography, algorithms and computational complexity,...
verified that
is 1 for in 1993, but the conjecture remains an open problem.See also
- Difference operator
- Prime gap
- Rule 90Rule 90Rule 90 is an elementary cellular automaton based on the exclusive or function. It consists of a one-dimensional array of cells, each of which can hold either a 0 or a 1 value; in each time step all values are simultaneously replaced by the exclusive or of the two neighboring values...
, a cellular automatonCellular automatonA cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
that controls the behavior of the parts of the rows that contain only the values 0 and 2