
Gossen's second law
Encyclopedia
Gossen's Second “Law”, named for Hermann Heinrich Gossen
(1810–1858), is the assertion that an economic
agent will allocate his or her expenditures such that the ratio of the marginal utility
of each good or service to its price (the marginal expenditure necessary for its acquisition) is equal to that for every other good or service. Formally,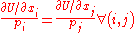
where
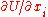 is well defined
is well defined
for each good or service. An agent then optimizes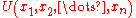
subject to a budget constraint
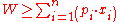
where
Using the method of Lagrange multipliers
, one constructs the function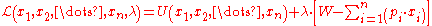
and finds the first-order conditions for optimization as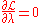
(which simply implies that all of will be spent) and
will be spent) and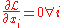
so that
which is algebraically equivalent to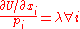
Since every such ratio is equal to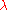 , the ratios are all equal one to another:
, the ratios are all equal one to another: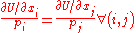
(Note that, as with any maximization using first-order conditions, the equations will hold only if the utility function satisfies specific concavity requirements and does not have maxima on the edges of the set over which one is maximizing.)
Hermann Heinrich Gossen
Hermann Heinrich Gossen was a Prussian economist who is often regarded as the first to elaborate a general theory of marginal utility.-Life and work:...
(1810–1858), is the assertion that an economic
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
agent will allocate his or her expenditures such that the ratio of the marginal utility
Marginal utility
In economics, the marginal utility of a good or service is the utility gained from an increase in the consumption of that good or service...
of each good or service to its price (the marginal expenditure necessary for its acquisition) is equal to that for every other good or service. Formally,
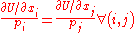
where
-
 is utilityUtilityIn economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
is utilityUtilityIn economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service.... -
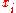 is quantity of the
is quantity of the 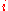 -th good or service
-th good or service -
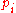 is the price of the
is the price of the 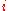 -th good or service
-th good or service
Informal derivation
Imagine that an agent has spent money on various sorts of goods or services. If the last unit of currency spent on goods or services of one sort bought a quantity with less marginal utility than that which would have been associated with the quantity of another sort that could have been bought with the money, then the agent would have been better off instead buying more of that other good or service. Assuming that goods and services are continuously divisible, the only way that it is possible that the marginal expenditure on one good or service should not yield more utility than the marginal expenditure on the other (or vice versa) is if the marginal expenditures yield equal utility.Formal derivation
Assume that utility, goods, and services have the requisite properties so that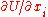 is well defined
is well definedWell-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
for each good or service. An agent then optimizes
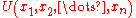
subject to a budget constraint
Budget constraint
A budget constraint represents the combinations of goods and services that a consumer can purchase given current prices with his or her income. Consumer theory uses the concepts of a budget constraint and a preference map to analyze consumer choices...
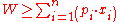
where
-
 is the total available sum of money
is the total available sum of money
Using the method of Lagrange multipliers
Lagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
, one constructs the function
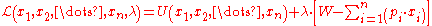
and finds the first-order conditions for optimization as
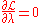
(which simply implies that all of
 will be spent) and
will be spent) and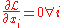
so that

which is algebraically equivalent to
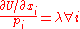
Since every such ratio is equal to
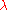 , the ratios are all equal one to another:
, the ratios are all equal one to another: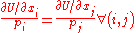
(Note that, as with any maximization using first-order conditions, the equations will hold only if the utility function satisfies specific concavity requirements and does not have maxima on the edges of the set over which one is maximizing.)
See also
- Gossen's lawsGossen's lawsGossen's laws, named for Hermann Heinrich Gossen , are three ostensible laws of economics:* Gossen's First Law is the “law” of diminishing marginal utility: that marginal utilities are diminishing across the ranges relevant to decision-making.* Gossen's Second Law, which presumes that utility is at...
- Hermann Heinrich GossenHermann Heinrich GossenHermann Heinrich Gossen was a Prussian economist who is often regarded as the first to elaborate a general theory of marginal utility.-Life and work:...
- Marginal utilityMarginal utilityIn economics, the marginal utility of a good or service is the utility gained from an increase in the consumption of that good or service...
- MarginalismMarginalismMarginalism refers to the use of marginal concepts in economic theory. Marginalism is associated with arguments concerning changes in the quantity used of a good or service, as opposed to some notion of the over-all significance of that class of good or service, or of some total quantity...

