Gromov's inequality for complex projective space

Riemannian geometry

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...

, Gromov's optimal stable 2-systolic inequality is the inequality

,

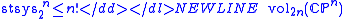valid for an arbitrary Riemannian metric on the complex projective space

Complex projective space

In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...

, where the optimal bound is attained
by the symmetric Fubini-Study metric

Fubini-Study metric

In mathematics, the Fubini–Study metric is a Kähler metric on projective Hilbert space, that is, complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study....

, providing a natural geometrisation of quantum mechanics

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

. Here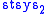

is the stable 2-systole, which in this case can be defined as the infimum of the areas of rational 2-cycles representing the class of the complex projective line

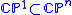in 2-dimensional homology.

The inequality first appeared in Gromov's 1981 book entitled Structures métriques pour les variétés riemanniennes (Theorem 4.36).

The proof of Gromov's inequality relies on the Wirtinger inequality for exterior 2-forms

Wirtinger inequality (2-forms)

In mathematics, the Wirtinger inequality for 2-forms, named after Wilhelm Wirtinger, states that the exterior \scriptstyle\nuth power of the standard symplectic form ω, when evaluated on a simple -vector ζ of unit volume, is bounded above by \scriptstyle\nu!...

Projective planes over division algebras

In the special case n=2, Gromov's inequality becomes

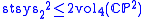. This inequality can be thought of as an analog of Pu's inequality for the real projective plane

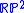. In both cases, the boundary case of equality is attained by the symmetric metric of the projective plane. Meanwhile, in the quaternionic case, the symmetric metric on

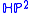is not its systolically optimal metric. In other words, the manifold

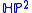admits Riemannian metrics with higher systolic ratio

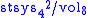than for its symmetric metric, see Bangert et al (2009).

Projective planes over division algebras

See also