
Harish-Chandra's c-function
Encyclopedia
In mathematics, Harish-Chandra's c-function is a function related to the intertwining operator between two principal series representations, that appears in the Plancherel measure
for semisimple Lie groups. introduced a special case of it defined in terms of the asymptotic behavior of a zonal spherical function
of a Lie group, and introduced a more general c-function called Harish-Chandra's (generalized) C-function. introduced the Gindikin–Karpelevich formula, a product formula for Harish-Chandra's c-function,.
The unique element of greatest length
s0, is the unique element that carries the Weyl chamber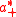 onto
onto 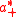 . By Harish-Chandra's integral formula, cs0 is Harish-Chandra's c-function:
. By Harish-Chandra's integral formula, cs0 is Harish-Chandra's c-function:
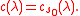
The c-functions are in general defined by the equation
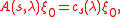
where ξ0 is the constant function 1 in L2(K/M). The cocycle property of the intertwining operators implies a similar multiplicative property for the c-functions:
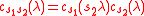
provided

This reduces the computation of cs to the case when s = sα, the reflection in a (simple) root α, the so-called
"rank-one reduction" of . In fact the integral involves only the closed connected subgroup Gα corresponding to the Lie subalgebra generated by where α lies in Σ0+. Then Gα is a real semisimple Lie group with real rank one, i.e. dim Aα = 1,
where α lies in Σ0+. Then Gα is a real semisimple Lie group with real rank one, i.e. dim Aα = 1,
and cs is just the Harish-Chandra c-function of Gα. In this case the c-function can be computed directly and is given by
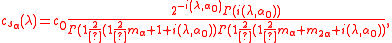
where
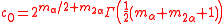
and α0=α/〈α,α〉.
The general Gindikin–Karpelevich formula for c(λ) is an immediate consequence of this formula and the multiplicative properties of cs(λ), as follows: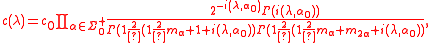
where the constant c0 is chosen so that c(–iρ)=1 .
, and the Plancherel measure is 1/c2 times Lebesgue measure.
and found an analogous product formula for the c-function of a p-adic Lie group.
Plancherel measure
In mathematics, Plancherel measure is a probability measure defined on the set of irreducible representations of a finite group G. In some cases the term Plancherel measure is applied specifically in the context of the group G being the finite symmetric group S_n – see below...
for semisimple Lie groups. introduced a special case of it defined in terms of the asymptotic behavior of a zonal spherical function
Zonal spherical function
In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G...
of a Lie group, and introduced a more general c-function called Harish-Chandra's (generalized) C-function. introduced the Gindikin–Karpelevich formula, a product formula for Harish-Chandra's c-function,.
Gindikin–Karpelevich formula
The c-function has a generalization cw(λ) depending on an element w of the Weyl group.The unique element of greatest length
s0, is the unique element that carries the Weyl chamber
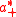 onto
onto 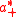 . By Harish-Chandra's integral formula, cs0 is Harish-Chandra's c-function:
. By Harish-Chandra's integral formula, cs0 is Harish-Chandra's c-function: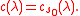
The c-functions are in general defined by the equation
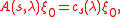
where ξ0 is the constant function 1 in L2(K/M). The cocycle property of the intertwining operators implies a similar multiplicative property for the c-functions:
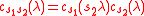
provided

This reduces the computation of cs to the case when s = sα, the reflection in a (simple) root α, the so-called
"rank-one reduction" of . In fact the integral involves only the closed connected subgroup Gα corresponding to the Lie subalgebra generated by
 where α lies in Σ0+. Then Gα is a real semisimple Lie group with real rank one, i.e. dim Aα = 1,
where α lies in Σ0+. Then Gα is a real semisimple Lie group with real rank one, i.e. dim Aα = 1,and cs is just the Harish-Chandra c-function of Gα. In this case the c-function can be computed directly and is given by
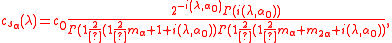
where
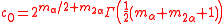
and α0=α/〈α,α〉.
The general Gindikin–Karpelevich formula for c(λ) is an immediate consequence of this formula and the multiplicative properties of cs(λ), as follows:
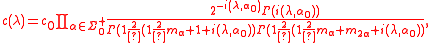
where the constant c0 is chosen so that c(–iρ)=1 .
Plancherel measure
The c-function appears in the Plancherel theorem for spherical functionsPlancherel theorem for spherical functions
In mathematics, the Plancherel theorem for spherical functions is an important result in the representation theory of semisimple Lie groups, due in its final form to Harish-Chandra...
, and the Plancherel measure is 1/c2 times Lebesgue measure.
p-adic Lie groups
There is a similar c-function for p-adic Lie groups.and found an analogous product formula for the c-function of a p-adic Lie group.

