
Hasse's theorem on elliptic curves
Encyclopedia
In mathematics
, Hasse's theorem on elliptic curves bounds the number of points on an elliptic curve
over a finite field
, above and below.
If N is the number of points on the elliptic curve E over a finite field with q elements, then Helmut Hasse
's result states that
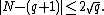
This had been a conjecture of Emil Artin
. It is equivalent to the determination of the absolute value
of the roots of the local zeta-function
of E.
That is, the interpretation is that N differs from q + 1, the number of points of the projective line
over the same field, by an 'error term' that is the sum of two complex number
s, each of absolute value √q.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Hasse's theorem on elliptic curves bounds the number of points on an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, above and below.
If N is the number of points on the elliptic curve E over a finite field with q elements, then Helmut Hasse
Helmut Hasse
Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
's result states that
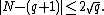
This had been a conjecture of Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
. It is equivalent to the determination of the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the roots of the local zeta-function
Local zeta-function
In number theory, a local zeta-functionis a function whose logarithmic derivative is a generating functionfor the number of solutions of a set of equations defined over a finite field F, in extension fields Fk of F.-Formulation:...
of E.
That is, the interpretation is that N differs from q + 1, the number of points of the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
over the same field, by an 'error term' that is the sum of two complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, each of absolute value √q.

