
Heine's identity
Encyclopedia
In mathematical analysis
, Heine's identity, named after Heinrich Eduard Heine is a Fourier expansion of a reciprocal square root
which Heine presented as

where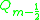 is a Legendre function
is a Legendre function
of the second kind, which has degree, m − 1/2, a half-integer, and argument, z, real and greater than one. This expression can be generalized for arbitrary half-integer powers as follows
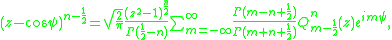
where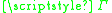 is the Gamma function
is the Gamma function
.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Heine's identity, named after Heinrich Eduard Heine is a Fourier expansion of a reciprocal square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
which Heine presented as

where
 is a Legendre function
is a Legendre functionLegendre function
In mathematics, the Legendre functions Pλ, Qλ and associated Legendre functions P, Q are generalizations of Legendre polynomials to non-integer degree.-Differential equation:...
of the second kind, which has degree, m − 1/2, a half-integer, and argument, z, real and greater than one. This expression can be generalized for arbitrary half-integer powers as follows
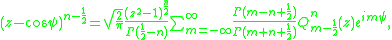
where
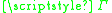 is the Gamma function
is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.

