Hilbert's seventeenth problem
Encyclopedia
Hilbert's seventeenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert
. It entails expression of definite rational function
s as quotient
s of sum
s of squares. Original Hilbert's question was:
Given a multivariate polynomial that takes only non-negative values over the reals, can it be represented as a sum of squares of rational functions?
This was solved in the affirmative, in 1927, by Emil Artin
.
An algorithm was later found by Charles Delzell: see his article "A continuous, constructive solution to Hilbert's 17th problem."
A generalization to the matrix case (matrices with rational function entries that are always positive semidefinite are sums of symmetric squares) was given by Gondard, Ribenboim and Procesi, Schacher , with an elementary proof given by Hillar and Nie .
The formulation of the question takes into account that there are polynomials, for example
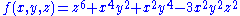
which are non-negative over reals and yet which cannot be represented as a sum of squares of other polynomials. This example was taken from:
Marie-Françoise Roy. The role of Hilbert's problems in real algebraic geometry.
Proceedings of the ninth EWM Meeting, Loccum, Germany 1999.
Explicit sufficient conditions for a polynomial f to be a sum of squares of other polynomials were found (http://www.optimization-online.org/DB_HTML/2007/02/1587.html, http://www.mathcs.emory.edu/~vicki/pub/sos.pdf). However every real nonnegative polynomial f can be approximated as closely as desired (in the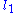
-norm of its coefficient vector) by a sequence of polynomials 
that are sums of squares of polynomials http://portal.acm.org/citation.cfm?id=1330215.1330223&coll=GUIDE&dl=.
It is an open question what is the smallest number
,
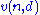such that any n-variate, non-negative polynomial of degree d can be written as sum of at most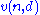
square rational functions over the reals.
The best known result is
;
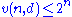for details see:
A. Pfister. Zur Darstellung definiter Funktionen als Summe von Quadraten. Invent.
Math. 4 (1967), 229–237
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
. It entails expression of definite rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s as quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
s of sum
SUM
SUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
s of squares. Original Hilbert's question was:
Given a multivariate polynomial that takes only non-negative values over the reals, can it be represented as a sum of squares of rational functions?
This was solved in the affirmative, in 1927, by Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
.
An algorithm was later found by Charles Delzell: see his article "A continuous, constructive solution to Hilbert's 17th problem."
A generalization to the matrix case (matrices with rational function entries that are always positive semidefinite are sums of symmetric squares) was given by Gondard, Ribenboim and Procesi, Schacher , with an elementary proof given by Hillar and Nie .
The formulation of the question takes into account that there are polynomials, for example
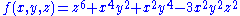
which are non-negative over reals and yet which cannot be represented as a sum of squares of other polynomials. This example was taken from:
Marie-Françoise Roy. The role of Hilbert's problems in real algebraic geometry.
Proceedings of the ninth EWM Meeting, Loccum, Germany 1999.
Explicit sufficient conditions for a polynomial f to be a sum of squares of other polynomials were found (http://www.optimization-online.org/DB_HTML/2007/02/1587.html, http://www.mathcs.emory.edu/~vicki/pub/sos.pdf). However every real nonnegative polynomial f can be approximated as closely as desired (in the
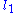-norm of its coefficient vector) by a sequence of polynomials that are sums of squares of polynomials http://portal.acm.org/citation.cfm?id=1330215.1330223&coll=GUIDE&dl=.It is an open question what is the smallest number
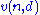,such that any n-variate, non-negative polynomial of degree d can be written as sum of at most
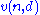square rational functions over the reals.The best known result is
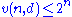;for details see:
A. Pfister. Zur Darstellung definiter Funktionen als Summe von Quadraten. Invent.
Math. 4 (1967), 229–237