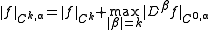Hölder condition
Encyclopedia
In mathematics
, a real or complex-valued function ƒ on d-dimensional Euclidean space
satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C,
, such that
for all x and y in the domain of ƒ. More generally, the condition can be formulated for functions between any two metric space
s. The number
is called the exponent of the Hölder condition. If 
= 1, then the function satisfies a Lipschitz condition. If 
= 0, then the function simply is bounded
. The condition is named after Otto Hölder
.
relevant to solving partial differential equations, and in dynamical system
s. The Hölder space
, where 
is an open subset of some Euclidean space and k ≥ 0 an integer, consists of those functions on 
having continuous derivative
s up to order k and such that the kth partial derivatives are Hölder continuous with exponent
, where 0 < 
≤ 1. This is a locally convex topological vector space
. If the Hölder coefficient
is finite, then the function ƒ is said to be (uniformly) Hölder continuous with exponent
in 
. In this case, Hölder coefficient serves as a seminorm. If the Hölder coefficient is merely bounded on compact subsets of Ω, then the function ƒ is said to be locally Hölder continuous with exponent α in Ω.
If the function ƒ and its derivatives up to order k are bounded on the closure of Ω, then the Hölder space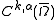
can be assigned the norm
where β ranges over multi-indices
and
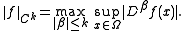
These norms and seminorms are often denoted simply
and 
or also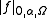 
and 
in order to stress the dependence on the domain of f. If 
is open and bounded, then 
is a Banach space
with respect to the norm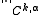
.
which is continuous since, by definition of the Hölder norms, the inequality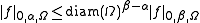
holds for all
Moreover, this inclusion is compact, meaning that bounded sets in the 
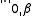norm are relatively compact in the 
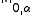norm. This is a direct consequence of the Ascoli-Arzelà theorem. Indeed, let 
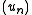be a bounded sequence in 
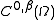. Thanks to the Ascoli-Arzelà theorem we can assume without loss of generality that 
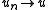uniformly, and we can also assume 
. Then 
because
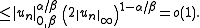
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a real or complex-valued function ƒ on d-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C,
, such that
for all x and y in the domain of ƒ. More generally, the condition can be formulated for functions between any two metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. The number
is called the exponent of the Hölder condition. If = 1, then the function satisfies a Lipschitz condition. If = 0, then the function simply is boundedBounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
. The condition is named after Otto Hölder
Otto Hölder
Otto Ludwig Hölder was a German mathematician born in Stuttgart.Hölder first studied at the Polytechnikum and then in 1877 went to Berlin where he was a student of Leopold Kronecker, Karl Weierstraß, and Ernst Kummer.He is famous for many things including: Hölder's inequality, the Jordan–Hölder...
.
Hölder spaces
Hölder spaces consisting of functions satisfying a Hölder condition are basic in areas of functional analysisFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
relevant to solving partial differential equations, and in dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s. The Hölder space
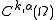, where is an open subset of some Euclidean space and k ≥ 0 an integer, consists of those functions on 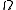having continuous derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s up to order k and such that the kth partial derivatives are Hölder continuous with exponent
, where 0 < ≤ 1. This is a locally convex topological vector spaceTopological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
. If the Hölder coefficient
is finite, then the function ƒ is said to be (uniformly) Hölder continuous with exponent
in 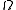. In this case, Hölder coefficient serves as a seminorm. If the Hölder coefficient is merely bounded on compact subsets of Ω, then the function ƒ is said to be locally Hölder continuous with exponent α in Ω.If the function ƒ and its derivatives up to order k are bounded on the closure of Ω, then the Hölder space
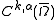can be assigned the norm
where β ranges over multi-indices
Multi-index notation
The mathematical notation of multi-indices simplifies formulae used in multivariable calculus, partial differential equations and the theory of distributions, by generalising the concept of an integer index to an ordered tuple of indices....
and
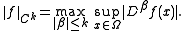
These norms and seminorms are often denoted simply
and or also 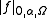and in order to stress the dependence on the domain of f. If is open and bounded, then is a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
with respect to the norm
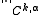.Compact embedding of Hölder spaces
Let Ω be a bounded subset of some Euclidean space (or more generally, any totally bounded metric space) and let 0 < α < β ≤ 1 two Hölder exponents. Then, there is an obvious inclusion of the corresponding Hölder spaces:which is continuous since, by definition of the Hölder norms, the inequality
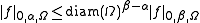
holds for all
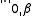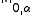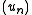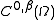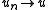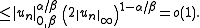
Moreover, this inclusion is compact, meaning that bounded sets in the norm are relatively compact in the norm. This is a direct consequence of the Ascoli-Arzelà theorem. Indeed, let be a bounded sequence in . Thanks to the Ascoli-Arzelà theorem we can assume without loss of generality that uniformly, and we can also assume . Then because Examples
- If 0 < α ≤ β ≤ 1 then all
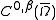Hölder continuous functions on a bounded set 
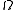are also 
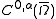Hölder continuous. This also includes β = 1 and therefore all Lipschitz continuousLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
functions on a bounded set are also
Hölder continuous.
- The function
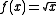defined on [0, 1] is not Lipschitz continuous, but is 
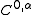Hölder continuous for α ≤ 1/2.
- In the same manner, the function
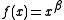(with β ≤1) defined on [0, 1] serves as a prototypical example of a function that is 
Hölder continuous for 0 < α ≤ β, but not for α > β.
- There are examples of uniformly continuous functions that are not α–Hölder continuous for any α. For instance, the function defined on [0,1/2] by
and by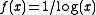 
otherwise is continuous, and therefore uniformly continuous. It does not satisfy a Hölder condition of any order, however.
- For α > 1, any α–Hölder continuous function on [0, 1] is a constant.
- Peano curves from [0, 1] onto the square [0, 1]2 can be constructed to be 1/2–Hölder continuous. It can be proved that when α > 1/2, the image of a α–Hölder continuous function from the unit interval to the square cannot fill the square.
- A closed additive subgroup of an infinite dimensional Hilbert space H, connected by α–Hölder continuous arcs with α > 1/2, is a linear subspace. There are closed additive subgroups of H, not linear subspaces, connected by 1/2–Hölder continuous arcs. An example is the additive subgroup
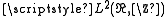of the Hilbert space 
.
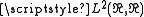- Any α–Hölder continuous function
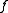on a metric space 
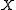admits a Lipschitz approximation by means of a sequence of functions 
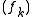such that 
is 
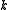-Lipschitz and 
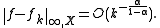Conversely, any such sequence 
of Lipschitz functions converges to an α–Hölder continuous uniform limit 
.
- Any α–Hölder function
on a subset 
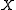of a normed space 
admits a uniformly continuous extension to the whole space, which is Hölder continuous with the same constant C and the same exponent α. The larger such extension is: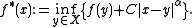
- Functions in Sobolev spaceSobolev spaceIn mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
can be embedded into the appropriate Hölder space via Morrey's inequality if the spatial dimension is less than the exponent of the Sobolev space. To be precise, if n < p ≤ ∞ then there exists a constant C, depending only on p and n, such that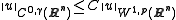
for all u ∈ C1 (Rn) ∩ Lp(Rn), where 
Thus if u ∈ W1,p(Rn), then u is in fact Hölder continuous of exponent γ, after possibly being redefined on a set of measure 0.
- Functions which are locally integrable and whose integrals satisfy an appropriate growth condition are also Hölder continuous. For example, if we let
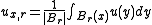and u satisfies 
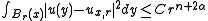, then u is Hölder continuous with exponent 
.
- Functions whose oscillation decay at a fixed rate with respect to distance are Hölder continuous with an exponent that is determined by the rate of decay. For instance, if
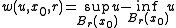for some function 
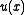satisfies 
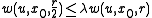for a fixed 
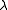with 
and all sufficiently small values of r, then u is Hölder continuous.