
Jacobi's four-square theorem
Encyclopedia
In 1834, Carl Gustav Jakob Jacobi
found an exact formula for the total number of ways a given positive integer n can be represented as the sum of four squares. Two representations are considered different if their terms are in different order or if the integer being squared (not just the square) is different; to illustrate, these are three of the eight different ways to represent 1:
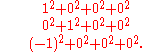
The number of ways to represent n as the sum of four squares is eight times the sum of the divisor
s of n if n is odd and 24 times the sum of the odd divisors of n if n is even (see divisor function
), i.e.
Carl Gustav Jakob Jacobi
Carl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
found an exact formula for the total number of ways a given positive integer n can be represented as the sum of four squares. Two representations are considered different if their terms are in different order or if the integer being squared (not just the square) is different; to illustrate, these are three of the eight different ways to represent 1:
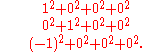
The number of ways to represent n as the sum of four squares is eight times the sum of the divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s of n if n is odd and 24 times the sum of the odd divisors of n if n is even (see divisor function
Divisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
), i.e.
-

Equivalently, it is eight times the sum of all its divisors which are not divisible by 4, i.e.
In particular, for a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p we have the explicit formula r4(p) = 8(p + 1).
The proof shows that the Theta series for the latticeLattice (discrete subgroup)In Lie theory and related areas of mathematics, a lattice in a locally compact topological group is a discrete subgroup with the property that the quotient space has finite invariant measure...
Z4 is a modular formModular formIn mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
of a certain level, and hence equals a linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of Eisenstein seriesEisenstein seriesEisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
.
External links
-


