Jefimenko's equations
Encyclopedia
In electromagnetism
, Jefimenko's equations (named after Oleg D. Jefimenko
) describe the behavior of the electric
and magnetic field
s in terms of the charge
and current
distributions at retarded times.
Jefimenko's equations are the solution of Maxwell's equations
for an assigned distribution of electric charges and currents, under the assumption that there is no electromagnetic field other than the one produced by those charges and currents, that is no electromagnetic field coming from the infinite past.
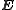and the magnetic field 
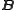produced by an arbitrary charge distribution of charge density
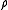and current density
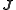are:
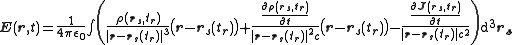
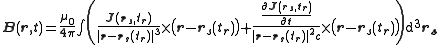
where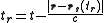
(the retarded time).
and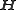 
have similar expressions .
) However, Jefimenko's equations show otherwise. Jefimenko says, "...neither Maxwell's equations nor their solutions indicate an existence of causal links between electric and magnetic fields. Therefore, we must conclude that an electromagnetic field is a dual entity always having an electric and a magnetic component simultaneously created by their common sources: time-variable electric charges and currents."
As pointed out by McDonald, Jefimenko's equations seem to appear first in 1962 in the second edition of Panofsky and Phillips's classic textbook. Essential features of these equations are easily observed which is that the right hand sides involve "retarded" time which reflects the "causality" of the expressions. In other words, the left side of each equation is actually "caused" by the right side, unlike the normal differential expressions for Maxwell's equations where both sides take place simultaneously. In the typical expressions for Maxwell's equations there is no doubt that both sides are are equal to each other, but as Jefimenko notes, "... since each of these equations connects quantities simultaneous in time, none of these equations can represent a causal relation." The second feature is that the expression for E does not depend upon B and vice versa. Hence, it is impossible for E and B fields to be "creating" each other. Charge density and current density are creating them both.
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, Jefimenko's equations (named after Oleg D. Jefimenko
Oleg D. Jefimenko
Oleg Dmitrovich Jefimenko - physicist and Professor Emeritus at West Virginia University.-Biography:...
) describe the behavior of the electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s in terms of the charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
and current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
distributions at retarded times.
Jefimenko's equations are the solution of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
for an assigned distribution of electric charges and currents, under the assumption that there is no electromagnetic field other than the one produced by those charges and currents, that is no electromagnetic field coming from the infinite past.
Electric and magnetic fields
The electric field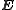 and the magnetic field 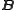produced by an arbitrary charge distribution of charge densityCharge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
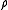and current densityCurrent density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
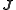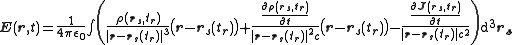
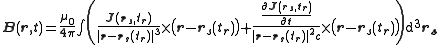
are:where
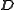(the retarded time). and 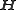have similar expressions .Discussion
There is a widespread interpretation of Maxwell's equations indicating that time variable electric and magnetic fields can cause each other. This is often used as part of an explanation of the formation of electromagnetic waves. (electromagnetismElectromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
) However, Jefimenko's equations show otherwise. Jefimenko says, "...neither Maxwell's equations nor their solutions indicate an existence of causal links between electric and magnetic fields. Therefore, we must conclude that an electromagnetic field is a dual entity always having an electric and a magnetic component simultaneously created by their common sources: time-variable electric charges and currents."
As pointed out by McDonald, Jefimenko's equations seem to appear first in 1962 in the second edition of Panofsky and Phillips's classic textbook. Essential features of these equations are easily observed which is that the right hand sides involve "retarded" time which reflects the "causality" of the expressions. In other words, the left side of each equation is actually "caused" by the right side, unlike the normal differential expressions for Maxwell's equations where both sides take place simultaneously. In the typical expressions for Maxwell's equations there is no doubt that both sides are are equal to each other, but as Jefimenko notes, "... since each of these equations connects quantities simultaneous in time, none of these equations can represent a causal relation." The second feature is that the expression for E does not depend upon B and vice versa. Hence, it is impossible for E and B fields to be "creating" each other. Charge density and current density are creating them both.