Kater's pendulum - AbsoluteAstronomy.com

A Kater's pendulum is a reversible freeswinging pendulum

Pendulum

A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...

invented by British physicist and army captain Henry Kater

Henry Kater

Henry Kater was an English physicist of German descent.-Early life:He was born at Bristol. At first he intended to study law; but he gave up the idea on his father's death in 1794. He entered the army, obtaining a commission in the 12th Regiment of Foot, then stationed in India, where he assisted...

in 1817 for use as a gravimeter

Gravimeter

A gravimeter or gravitometer is an instrument used in gravimetry for measuring the local gravitational field of the Earth. A gravimeter is a type of accelerometer, specialized for measuring the constant downward acceleration of gravity, which varies by about 0.5% over the surface of the Earth...

instrument to measure the local acceleration of gravity. Its advantage is that, unlike previous pendulum gravimetry methods, the pendulum's centre of gravity and center of oscillation don't have to be determined, allowing greater accuracy. For about a century, until the 1930s, Kater's pendulum and its various refinements remained the standard method for measuring the strength of the Earth's gravity during geodetic surveys. It is now used only for demonstrating pendulum principles.

Description

The pendulum consists of a rigid metal bar with two pivot points, one near each end of the bar. It can be suspended from either pivot and swung. It also has either an adjustable weight that can be moved up and down the bar, or one adjustable pivot, to adjust the periods of swing. In use, it is swung from one pivot, and the period

Frequency

Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...

timed, and then turned upside down and swung from the other pivot, and the period timed. The moveable weight (or pivot) is adjusted until the two periods are equal. At this point the period is equal to the period of an 'ideal' simple pendulum of length equal to the distance between the pivots. From the period and the measured distance between the pivots, the acceleration of gravity can be calculated with great precision from the periodicity equation for a simple pendulum, (1) below.

Gravity measurement with pendulums

A pendulum can be used to measure the acceleration of gravity g because its period

Frequency

of swing T depends only on g and its length L:

So by measuring the length L and period T of a pendulum, g can be calculated. The first person to discover that gravity varied over the Earth's surface was French scientist Jean Richer

Jean Richer

Jean Richer was a French astronomer and assistant of Giovanni Domenico Cassini.Between 1671 and 1673 he traveled to Cayenne at the request of the French Academy of Sciences to observe Mars during its perigee...

, who in 1671 was sent on an expedition to Cayenne

Cayenne

Cayenne is the capital of French Guiana, an overseas region and department of France located in South America. The city stands on a former island at the mouth of the Cayenne River on the Atlantic coast. The city's motto is "Ferit Aurum Industria" which means "Work brings wealth"...

, French Guiana

French Guiana

French Guiana is an overseas region of France, consisting of a single overseas department located on the northern Atlantic coast of South America. It has borders with two nations, Brazil to the east and south, and Suriname to the west...

by the French Académie des Sciences, assigned the task of making measurements with a pendulum clock

Pendulum clock

A pendulum clock is a clock that uses a pendulum, a swinging weight, as its timekeeping element. The advantage of a pendulum for timekeeping is that it is a resonant device; it swings back and forth in a precise time interval dependent on its length, and resists swinging at other rates...

. Through the observations he made in the following year, Richer determined that the clock was 2½ minutes per day slower than at Paris, or equivalently the length of a pendulum with a swing of one second there was 1¼ Paris lines, or 2.6 mm, shorter than at Paris. It was realized by the scientists of the day, and proven by Isaac Newton

Isaac Newton

Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...

in 1687, that this was due to the fact that the Earth was not a perfect sphere but slightly oblate; it was thicker at the equator because of the Earth's rotation. Since the surface was farther from the Earth's center at Cayenne than at Paris, gravity was weaker there. Since that time pendulums began to be used as precision gravimeter

Gravimeter

s, taken on voyages to different parts of the world to measure the local gravitational acceleration. The accumulation of geographical gravity data resulted in more and more accurate models of the overall shape of the Earth.

At that time, the local strength of gravity was usually expressed not by the value of the acceleration g which is now used, but by the length at that location of the seconds pendulum
Seconds pendulum
A seconds pendulum is a pendulum whose period is precisely two seconds; one second for a swing in one direction and one second for the return swing, a frequency of 1/2 Hz....

, a pendulum with a period of two seconds, so each swing takes one second. It can be seen from equation (1) that for a seconds pendulum, the length is simply proportional to g:

Inaccuracy of gravimeter pendulums

In Kater's time, the period T of pendulums could be measured very precisely by timing them with precision clocks set by the passage of stars overhead. Prior to Kater's discovery, the accuracy of g measurements was limited by the difficulty of measuring the other factor L, the length of the pendulum, accurately. L in equation (1) above was the length of an ideal mathematical 'simple pendulum' consisting of a point mass swinging on the end of a massless cord. However the 'length' of a real pendulum, a swinging rigid body, known in mechanics as a compound pendulum, is more difficult to define. In 1673 Dutch scientist Christiaan Huygens in his mathematical analysis of pendulums, Horologium Oscillatorium, showed that a real pendulum had the same period as a simple pendulum with a length equal to the distance between the pivot point and a point called the center of oscillation, which is located under the pendulum's center of gravity

Center of gravity

In physics, a center of gravity of a material body is a point that may be used for a summary description of gravitational interactions. In a uniform gravitational field, the center of mass serves as the center of gravity...

and depends on the mass distribution along the length of the pendulum. The problem was there was no way to find the location of the center of oscillation in a real pendulum accurately. It could theoretically be calculated from the shape of the pendulum if the metal parts had uniform density, but the metallurgical quality and mathematical abilities of the time didn't allow the calculation to be made accurately.

To get around this problem, most early gravity researchers, such as Jean Picard

Jean Picard

Jean-Felix Picard was a French astronomer and priest born in La Flèche, where he studied at the Jesuit Collège Royal Henry-Le-Grand. He was the first person to measure the size of the Earth to a reasonable degree of accuracy in a survey conducted in 1669–70, for which he is honored with a...

(1669), Charles Marie de la Condamine

Charles Marie de La Condamine

Charles Marie de La Condamine was a French explorer, geographer, and mathematician. He spent ten years in present-day Ecuador measuring the length of a degree latitude at the equator and preparing the first map of the Amazon region based on astronomical observations.-Biography:Charles Marie de La...

(1735), and Jean-Charles de Borda

Jean-Charles de Borda

Jean-Charles, chevalier de Borda was a French mathematician, physicist, political scientist, and sailor.-Life history:...

(1792) approximated a simple pendulum by using a metal sphere suspended by a light wire. If the wire had negligible mass, the center of oscillation was close to the center of gravity of the sphere. But even finding the center of gravity of the sphere accurately was difficult. In addition, this type of pendulum inherently wasn't very accurate. The sphere and wire didn't swing back and forth as a rigid unit, because the sphere acquired a slight angular momentum

Angular momentum

In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...

during each swing. Also the wire stretched elastically during the pendulum's swing, changing L slightly during the cycle.

Kater's solution

However, in Horologium Oscillatorium, Huygens had also proved that the pivot point and the center of oscillation were interchangeable. That is, if any pendulum is suspended upside down from its center of oscillation, it has the same period of swing, and the new center of oscillation is the old pivot point. The distance between these two conjugate points was equal to the length of a simple pendulum with the same period.

As part of a committee appointed by the Royal Society

Royal Society

The Royal Society of London for Improving Natural Knowledge, known simply as the Royal Society, is a learned society for science, and is possibly the oldest such society in existence. Founded in November 1660, it was granted a Royal Charter by King Charles II as the "Royal Society of London"...

to reform British measures, Kater had been contracted by the House of Commons to determine accurately the length of the seconds pendulum in London. He realized Huygens principle could be used to find the center of oscillation, and so the length L, of a rigid (compound) pendulum. If a pendulum were hung upside down from a second pivot point which could be adjusted up and down on the pendulum's rod, and the second pivot were adjusted until the pendulum had the same period as it did when swinging right side up from the first pivot, the second pivot would be at the center of oscillation, and the distance between the two pivot points would be L.

Kater wasn't the first to have this idea.
French mathematician Gaspard de Prony

Gaspard de Prony

Gaspard Clair François Marie Riche de Prony was a French mathematician and engineer, who worked on hydraulics. He was born at Chamelet, Beaujolais, France and died in Asnières-sur-Seine, France.-Education and early works:...

first proposed a reversible pendulum in 1800, but his work was not published till 1889. In 1811 Friedrich Bohnenberger again discovered it, but Kater independently invented it and was first to put it in practice.

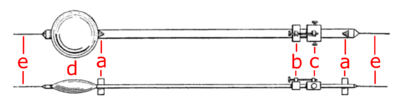
The pendulum

Kater built a pendulum consisting of a brass rod about 2 meters long, 1½ inches wide and one-eighth inch thick, with a weight (d) on one end. For a low friction pivot he used a pair of short triangular 'knife' blades attached to the rod. In use the pendulum was hung from a bracket on the wall, supported by the edges of the knife blades resting on flat agate plates. The pendulum had two of these knife blade pivots (a), facing one another, about a meter (40 in) apart, so that a swing of the pendulum took approximately one second when hung from each pivot.

Kater found that making one of the pivots adjustable caused inaccuracies, making it hard to keep the axis of both pivots precisely parallel. Instead he permanently attached the knife blades to the rod, and adjusted the periods of the pendulum by a small moveable weight (b,c) on the pendulum shaft. Since gravity only varies by a maximum of 0.5% over the Earth, and in most locations much less than that, the weight only had to be adjusted slightly. Moving the weight toward one of the pivots decreased the period when hung from that pivot, and increased the period when hung from the other pivot. This also had the advantage that the precision measurement of the separation between the pivots only had to be made once.

Experimental procedure

To use, the pendulum was hung in front of a precision pendulum clock to time the period. It was swung first from one pivot, and the oscillations timed, then turned upside down and swung from the other pivot, and the oscillations timed again. The small weight (c) was adjusted with the adjusting screw, and the process repeated until the pendulum had the same period when swung from each pivot. By putting the measured period T, and the measured distance between the pivot blades L, into the period equation (1), g could be calculated very accurately.

Kater performed 12 trials. He measured the period of his pendulum very accurately using the clock pendulum by the method of coincidences; timing the interval between the coincidences when the two pendulums were swinging in synchronism. He measured the distance between the pivot blades with a microscope comparator, to an accuracy of 10⁻⁴ in. (2.5 μm). As with other pendulum gravity measurements, he had to apply small corrections to the result for a number of variable factors:

the finite width of the pendulum's swing, which increased the period
temperature, which caused the length of the rod to vary due to thermal expansion
Thermal expansion
Thermal expansion is the tendency of matter to change in volume in response to a change in temperature.When a substance is heated, its particles begin moving more and thus usually maintain a greater average separation. Materials which contract with increasing temperature are rare; this effect is...
atmospheric pressure, which reduced the effective mass of the pendulum by the buoyancy of the displaced air, increasing the period
altitude, which reduced the gravitational force with distance from the center of the Earth. Gravity measurements are always referenced to sea level
Sea level
Mean sea level is a measure of the average height of the ocean's surface ; used as a standard in reckoning land elevation...

.

He gave his result as the length of the seconds pendulum

Seconds pendulum

A seconds pendulum is a pendulum whose period is precisely two seconds; one second for a swing in one direction and one second for the return swing, a frequency of 1/2 Hz....

. After corrections, he found that the mean length of the solar seconds pendulum at London, at sea level, at 62°F, swinging in vacuum, was 39.1386 inches. This is equivalent to a gravitational acceleration of 9.81158 m/s². The largest variation of his results from the mean was 0.00028 inch. This represented a precision of gravity measurement of 7(10⁻⁶) (7 milligals).

In 1824, the British Parliament made Kater's measurement of the seconds pendulum the official standard of length for defining the yard.

Use

The large increase in gravity measurement accuracy made possible by Kater's pendulum established gravimetry

Gravimetry

Gravimetry is the measurement of the strength of a gravitational field. Gravimetry may be used when either the magnitude of gravitational field or the properties of matter responsible for its creation are of interest...

as a regular part of geodesy

Geodesy

Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...

. To be useful, it was necessary to find the exact location (latitude and longitude) of the 'station' where a gravity measurement was taken, so pendulum measurements became part of surveying

Surveying

See Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...

. Kater's pendulums were taken on the great historic geodetic surveys of much of the world that were being done during the 19th century. In particular, Kater's pendulums were used in the Great Trigonometric Survey

Great Trigonometric Survey

The Great Trigonometric Survey was a project of the Survey of India throughout most of the 19th century. It was piloted in its initial stages by William Lambton, and later by George Everest. Among the many accomplishments of the Survey were the demarcation of the British territories in India and...

of India.

Reversible pendulums remained the standard method used for absolute gravity measurements until they were superseded by free-fall gravimeter

Gravimeter

s in the 1950s.

Repsold–Bessel pendulum

Repeatedly timing each period of a Kater pendulum, and adjusting the weights until they were equal, was time consuming and error-prone. Friedrich Bessel

Friedrich Bessel

-References:* John Frederick William Herschel, A brief notice of the life, researches, and discoveries of Friedrich Wilhelm Bessel, London: Barclay, 1847 -External links:...

showed in 1826 that this was unnecessary. As long as the periods measured from each pivot, T₁ and T₂, are close in value, the period T of the equivalent simple pendulum can be calculated from them:

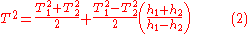
Here

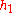and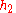

are the distances of the two pivots from the pendulum's center of gravity, so

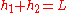, the separation of the pivots, which can be measured with great accuracy.

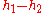cannot be measured with comparable accuracy. It is found by balancing the pendulum on a knife edge to find its center of gravity, measuring the distances of each of the pivots from the center of gravity, and subtracting. However, because

is so much smaller than

, the second term on the right in the above equation is small compared to the first, so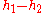

doesn't have to be determined with high accuracy, and the balancing procedure described above is sufficient to give accurate results.

Therefore the pendulum doesn't have to be adjustable at all, it can simply be a rod with two pivots. As long as each pivot is close to the center of oscillation of the other, so the two periods are close, the period T of the equivalent simple pendulum can be calculated with equation (2), and the gravity can be calculated from T and L with (1).

In addition, Bessel showed that if the pendulum was made with a symmetrical shape, but internally weighted on one end, the error caused by effects of air resistance would cancel out. Also, another error caused by the finite diameter of the pivot knife edges could be made to cancel out by interchanging the knife edges.

Bessel didn't construct such a pendulum, but in 1864 Adolf Repsold, under contract to the Swiss Geodetic Commission, developed a symmetric pendulum 56 cm long with interchangeable pivot blades, with a period of about 3/4 second. The Repsold pendulum was used extensively by the Swiss and Russian Geodetic agencies, and in the Survey of India

Great Trigonometric Survey

. Other widely used pendulums of this design were made by Charles Peirce and C. Defforges.

External links

The Accurate Measurement of g using Kater's pendulum, U. of Sheffield Has derivation of equations
Kater, Henry (June 1818) An Account of the Experiments for determining the length of the pendulum vibrating seconds in the latitude of London, The Edinburgh Review, Vol. 30, p.407 Has detailed account of experiment, description of pendulum , value determined, interest of French scientists

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.