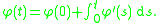Komura's theorem
Encyclopedia
In mathematics
, Kōmura's theorem is a result on the differentiability
of absolutely continuous
Banach space
-valued functions, and is a substantial generalization of Lebesgue's theorem on the differentiability of the indefinite integral, which is that Φ : [0, T] → R given by
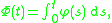
is differentiable at t for almost every
0 < t < T when φ : [0, T] → R lies in the Lp space
L1([0, T]; R).
Banach space and let φ : [0, T] → X be absolutely continuous. Then φ is (strongly) differentiable almost everywhere, the derivative φ′ lies in the Bochner space
L1([0, T]; X), and, for all 0 ≤ t ≤ T,
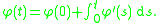
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Kōmura's theorem is a result on the differentiability
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of absolutely continuous
Absolute continuity
In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
-valued functions, and is a substantial generalization of Lebesgue's theorem on the differentiability of the indefinite integral, which is that Φ : [0, T] → R given by
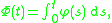
is differentiable at t for almost every
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
0 < t < T when φ : [0, T] → R lies in the Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
L1([0, T]; R).
Statement of the theorem
Let (X, || ||) be a reflexiveReflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
Banach space and let φ : [0, T] → X be absolutely continuous. Then φ is (strongly) differentiable almost everywhere, the derivative φ′ lies in the Bochner space
Bochner space
In mathematics, Bochner spaces are a generalization of the concept of Lp spaces to functions whose values lie in a Banach space which is not necessarily the space R or C of real or complex numbers....
L1([0, T]; X), and, for all 0 ≤ t ≤ T,