
Kummer's congruence
Encyclopedia
In mathematics, Kummer's congruences are some congruence
s involving Bernoulli numbers, found by .
used Kummer's congruences to define the p-adic zeta function.

where p is a prime, h and k are positive even integers not divisible by p−1, and the numbers Bh are Bernoulli numbers.
More generally if h and k are positive even integers not divisible by p − 1, then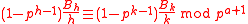
whenever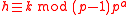
The two sides of the Kummer congruence are essentially values of the p-adic zeta function, and the Kummer congruences imply that the p-adic zeta function for negative integers is continuously, so can be extended by continuity to all p-adic integers.
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
s involving Bernoulli numbers, found by .
used Kummer's congruences to define the p-adic zeta function.
Statement
The simplest form of Kummer's congruence states that
where p is a prime, h and k are positive even integers not divisible by p−1, and the numbers Bh are Bernoulli numbers.
More generally if h and k are positive even integers not divisible by p − 1, then
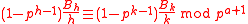
whenever
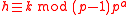
The two sides of the Kummer congruence are essentially values of the p-adic zeta function, and the Kummer congruences imply that the p-adic zeta function for negative integers is continuously, so can be extended by continuity to all p-adic integers.

