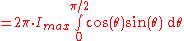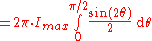
Lambert's cosine law
Encyclopedia
In optics
, Lambert's cosine law says that the radiant intensity
observed from a Lambertian surface
or a Lambertian radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal
. A Lambertian surface is also known as an ideal diffusely reflecting
surface. The law is also known as the cosine emission law or Lambert's emission law. It is named after Johann Heinrich Lambert
, from his Photometria, published in 1760.
An important consequence of Lambert's cosine law is that when a Lambertian surface is viewed from any angle, it has the same radiance
. This means, for example, that to the human eye it has the same apparent brightness (or luminance
). It has the same radiance because, although the emitted power from a given area element is reduced by the cosine of the emission angle, the apparent size (solid angle) of the observed area, as seen by a viewer, is decreased by a corresponding amount. Therefore, its radiance (power per unit solid angle per unit projected source area) is the same.
(energy or photons/time/area) landing on that area element will be proportional to the cosine of the angle between the illuminating source and the normal. A Lambertian scatterer will then scatter this light according to the same cosine law as a Lambertian emitter. This means that although the radiance of the surface depends on the angle from the normal to the illuminating source, it will not depend on the angle from the normal to the observer. For example, if the moon
were a Lambertian scatterer, one would expect to see its scattered brightness appreciably diminish towards the terminator
due to the increased angle at which sunlight hit the surface. The fact that it does not diminish illustrates that the moon is not a Lambertian scatterer, and in fact tends to scatter more light into the oblique angle
s than would a Lambertian scatterer.
The emission of a Lambertian radiator does not depend upon the amount of incident radiation, but rather from radiation originating in the emitting body itself. For example, if the sun
were a Lambertian radiator, one would expect to see a constant brightness across the entire solar disc. The fact that the sun exhibits limb darkening
in the visible region illustrates that it is not a Lambertian radiator. A black body
is an example of a Lambertian radiator.
s rather than energy
or luminous energy
. The wedges in the circle
each represent an equal angle dΩ, and for a Lambertian surface, the number of photons per second emitted into each wedge is proportional to the area of the wedge.
It can be seen that the length of each wedge is the product of the diameter
of the circle and cos(θ). It can also be seen that the maximum rate of photon emission per unit solid angle
is along the normal and diminishes to zero for θ = 90°. In mathematical terms, the radiance
along the normal is I photons/(s·cm2·sr) and the number of photons per second emitted into the vertical wedge is I dΩ dA. The number of photons per second emitted into the wedge at angle θ is I cos(θ) dΩ dA.
Figure 2 represents what an observer sees. The observer directly above the area element will be seeing the scene through an aperture of area dA0 and the area element dA will subtend a (solid) angle of dΩ0. We can assume without loss of generality that the aperture happens to subtend solid angle dΩ when "viewed" from the emitting area element. This normal observer will then be recording I dΩ dA photons per second and so will be measuring a radiance of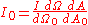
photons/(s·cm2·sr).
The observer at angle θ to the normal will be seeing the scene through the same aperture of area dA0 and the area element dA will subtend a (solid) angle of dΩ0 cos(θ). This observer will be recording I cos(θ) dΩ dA photons per second, and so will be measuring a radiance of
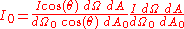photons/(s·cm2·sr),
which is the same as the normal observer.
of a point on a surface varies by direction; for a Lambertian surface, that distribution is defined by the cosine law, with peak luminous intensity in the normal direction. Thus when the Lambertian assumption holds, we can calculate the total luminous flux
,
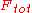, from the peak luminous intensity
,
, by integrating the cosine law:
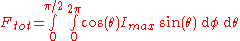
and so
where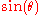
is the determinant of the Jacobian matrix for the unit sphere
, and realizing that
is luminous flux per steradian
. Similarly, the peak intensity will be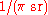
of the total radiated luminous flux. For Lambertian surfaces, the same factor of 
relates luminance
to luminous emittance, radiant intensity
to radiant flux
, and radiance
to radiant emittance. Radians and steradians are, of course, dimensionless and so "rad" and "sr" are included only for clarity.
Example: A surface with a luminance of say 100 cd/m2 (= 100 nits, typical PC-screen) seen from the front, will (if it is a perfect Lambert emitter) emit a total luminous flux of 314 lm/m2. If it's a 19" screen (area ≈ 0.1 m2), the total light emitted would thus be 31.4 lm.
This phenomenon is among others used when creating moldings
, which are a means of applying light and dark shaded stripes to a structure or object without having to change the material or apply pigment
. The contrast of dark and light areas gives definition to the object. Moldings are strips of material with various cross sections used to cover transitions between surfaces or for decoration.
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, Lambert's cosine law says that the radiant intensity
Radiant intensity
In radiometry, radiant intensity is a measure of the intensity of electromagnetic radiation. It is defined as power per unit solid angle. The SI unit of radiant intensity is watts per steradian . Radiant intensity is distinct from irradiance and radiant exitance, which are often called intensity...
observed from a Lambertian surface
Lambertian reflectance
If a surface exhibits Lambertian reflectance, light falling on it is scattered such that the apparent brightness of the surface to an observer is the same regardless of the observer's angle of view. More technically, the surface luminance is isotropic...
or a Lambertian radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
. A Lambertian surface is also known as an ideal diffusely reflecting
Diffuse reflection
Diffuse reflection is the reflection of light from a surface such that an incident ray is reflected at many angles rather than at just one angle as in the case of specular reflection...
surface. The law is also known as the cosine emission law or Lambert's emission law. It is named after Johann Heinrich Lambert
Johann Heinrich Lambert
Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
, from his Photometria, published in 1760.
An important consequence of Lambert's cosine law is that when a Lambertian surface is viewed from any angle, it has the same radiance
Radiance
Radiance and spectral radiance are radiometric measures that describe the amount of radiation such as light or radiant heat that passes through or is emitted from a particular area, and falls within a given solid angle in a specified direction. They are used to characterize both emission from...
. This means, for example, that to the human eye it has the same apparent brightness (or luminance
Luminance
Luminance is a photometric measure of the luminous intensity per unit area of light travelling in a given direction. It describes the amount of light that passes through or is emitted from a particular area, and falls within a given solid angle. The SI unit for luminance is candela per square...
). It has the same radiance because, although the emitted power from a given area element is reduced by the cosine of the emission angle, the apparent size (solid angle) of the observed area, as seen by a viewer, is decreased by a corresponding amount. Therefore, its radiance (power per unit solid angle per unit projected source area) is the same.
Lambertian scatterers and radiators
When an area element is radiating as a result of being illuminated by an external source, the irradianceIrradiance
Irradiance is the power of electromagnetic radiation per unit area incident on a surface. Radiant emittance or radiant exitance is the power per unit area radiated by a surface. The SI units for all of these quantities are watts per square meter , while the cgs units are ergs per square centimeter...
(energy or photons/time/area) landing on that area element will be proportional to the cosine of the angle between the illuminating source and the normal. A Lambertian scatterer will then scatter this light according to the same cosine law as a Lambertian emitter. This means that although the radiance of the surface depends on the angle from the normal to the illuminating source, it will not depend on the angle from the normal to the observer. For example, if the moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
were a Lambertian scatterer, one would expect to see its scattered brightness appreciably diminish towards the terminator
Terminator (solar)
A terminator, twilight zone or "grey line" is a moving line that separates the illuminated day side and the dark night side of a planetary body...
due to the increased angle at which sunlight hit the surface. The fact that it does not diminish illustrates that the moon is not a Lambertian scatterer, and in fact tends to scatter more light into the oblique angle
Oblique Angle
Oblique angle can refer to:*An angle which is not a multiple of 90°*Another word for "Dutch angle" in cinematography...
s than would a Lambertian scatterer.
The emission of a Lambertian radiator does not depend upon the amount of incident radiation, but rather from radiation originating in the emitting body itself. For example, if the sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
were a Lambertian radiator, one would expect to see a constant brightness across the entire solar disc. The fact that the sun exhibits limb darkening
Limb darkening
Limb darkening refers to the diminishing of intensity in the image of a star as one moves from the center of the image to the edge or "limb" of the image...
in the visible region illustrates that it is not a Lambertian radiator. A black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
is an example of a Lambertian radiator.
Details of equal brightness effect
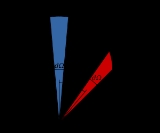
The situation for a Lambertian surface (emitting or scattering) is illustrated in Figures 1 and 2. For conceptual clarity we will think in terms of photonPhoton
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s rather than energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
or luminous energy
Luminous energy
In photometry, luminous energy is the perceived energy of light. This is sometimes also called the quantity of light.Luminous energy is not the same as the radiant energy, the corresponding objective physical quantity. This is because the human eye can only see light in the visible spectrum and has...
. The wedges in the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
each represent an equal angle dΩ, and for a Lambertian surface, the number of photons per second emitted into each wedge is proportional to the area of the wedge.
It can be seen that the length of each wedge is the product of the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of the circle and cos(θ). It can also be seen that the maximum rate of photon emission per unit solid angle
Solid angle
The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
is along the normal and diminishes to zero for θ = 90°. In mathematical terms, the radiance
Radiance
Radiance and spectral radiance are radiometric measures that describe the amount of radiation such as light or radiant heat that passes through or is emitted from a particular area, and falls within a given solid angle in a specified direction. They are used to characterize both emission from...
along the normal is I photons/(s·cm2·sr) and the number of photons per second emitted into the vertical wedge is I dΩ dA. The number of photons per second emitted into the wedge at angle θ is I cos(θ) dΩ dA.
Figure 2 represents what an observer sees. The observer directly above the area element will be seeing the scene through an aperture of area dA0 and the area element dA will subtend a (solid) angle of dΩ0. We can assume without loss of generality that the aperture happens to subtend solid angle dΩ when "viewed" from the emitting area element. This normal observer will then be recording I dΩ dA photons per second and so will be measuring a radiance of
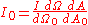photons/(s·cm2·sr).The observer at angle θ to the normal will be seeing the scene through the same aperture of area dA0 and the area element dA will subtend a (solid) angle of dΩ0 cos(θ). This observer will be recording I cos(θ) dΩ dA photons per second, and so will be measuring a radiance of
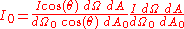photons/(s·cm2·sr),which is the same as the normal observer.
Relating peak luminous intensity and luminous flux
In general, the luminous intensityLuminous intensity
In photometry, luminous intensity is a measure of the wavelength-weighted power emitted by a light source in a particular direction per unit solid angle, based on the luminosity function, a standardized model of the sensitivity of the human eye...
of a point on a surface varies by direction; for a Lambertian surface, that distribution is defined by the cosine law, with peak luminous intensity in the normal direction. Thus when the Lambertian assumption holds, we can calculate the total luminous flux
Luminous flux
In photometry, luminous flux or luminous power is the measure of the perceived power of light. It differs from radiant flux, the measure of the total power of light emitted, in that luminous flux is adjusted to reflect the varying sensitivity of the human eye to different wavelengths of...
,
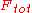, from the peak luminous intensityLuminous intensity
In photometry, luminous intensity is a measure of the wavelength-weighted power emitted by a light source in a particular direction per unit solid angle, based on the luminosity function, a standardized model of the sensitivity of the human eye...
,
, by integrating the cosine law: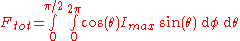
and so
where
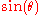is the determinant of the Jacobian matrix for the unit sphereUnit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
, and realizing that
is luminous flux per steradianSteradian
The steradian is the SI unit of solid angle. It is used to describe two-dimensional angular spans in three-dimensional space, analogous to the way in which the radian describes angles in a plane...
. Similarly, the peak intensity will be
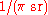of the total radiated luminous flux. For Lambertian surfaces, the same factor of relates luminanceLuminance
Luminance is a photometric measure of the luminous intensity per unit area of light travelling in a given direction. It describes the amount of light that passes through or is emitted from a particular area, and falls within a given solid angle. The SI unit for luminance is candela per square...
to luminous emittance, radiant intensity
Radiant intensity
In radiometry, radiant intensity is a measure of the intensity of electromagnetic radiation. It is defined as power per unit solid angle. The SI unit of radiant intensity is watts per steradian . Radiant intensity is distinct from irradiance and radiant exitance, which are often called intensity...
to radiant flux
Radiant flux
In radiometry, radiant flux or radiant power is the measure of the total power of electromagnetic radiation...
, and radiance
Radiance
Radiance and spectral radiance are radiometric measures that describe the amount of radiation such as light or radiant heat that passes through or is emitted from a particular area, and falls within a given solid angle in a specified direction. They are used to characterize both emission from...
to radiant emittance. Radians and steradians are, of course, dimensionless and so "rad" and "sr" are included only for clarity.
Example: A surface with a luminance of say 100 cd/m2 (= 100 nits, typical PC-screen) seen from the front, will (if it is a perfect Lambert emitter) emit a total luminous flux of 314 lm/m2. If it's a 19" screen (area ≈ 0.1 m2), the total light emitted would thus be 31.4 lm.
Uses
Lambert's cosine law in its reversed form (Lambertian reflection) implies that the apparent brightness of a Lambertian surface is proportional to cosine of the angle between the surface normal and the direction of the incident light.This phenomenon is among others used when creating moldings
Molding (decorative)
Molding or moulding is a strip of material with various profiles used to cover transitions between surfaces or for decoration. It is traditionally made from solid milled wood or plaster but may be made from plastic or reformed wood...
, which are a means of applying light and dark shaded stripes to a structure or object without having to change the material or apply pigment
Pigment
A pigment is a material that changes the color of reflected or transmitted light as the result of wavelength-selective absorption. This physical process differs from fluorescence, phosphorescence, and other forms of luminescence, in which a material emits light.Many materials selectively absorb...
. The contrast of dark and light areas gives definition to the object. Moldings are strips of material with various cross sections used to cover transitions between surfaces or for decoration.
See also
- TransmittanceTransmittanceIn optics and spectroscopy, transmittance is the fraction of incident light at a specified wavelength that passes through a sample. A related term is absorptance, or absorption factor, which is the fraction of radiation absorbed by a sample at a specified wavelength...
- ReflectivityReflectivityIn optics and photometry, reflectivity is the fraction of incident radiation reflected by a surface. In general it must be treated as a directional property that is a function of the reflected direction, the incident direction, and the incident wavelength...
- Passive solar building designPassive solar building designIn passive solar building design, windows, walls, and floors are made to collect, store, and distribute solar energy in the form of heat in the winter and reject solar heat in the summer...
- Sun pathSun pathSun path refers to the apparent significant seasonal-and-hourly positional changes of the sun as the Earth rotates, and orbits around the sun. The relative position of the sun is a major factor in the heat gain of buildings and in the performance of solar energy systems...