Lauricella's theorem
Encyclopedia
In the theory of orthogonal functions
, Lauricella's theorem provides a condition for checking the closure of a set of orthogonal functions, namely:
Theorem. A necessary and sufficient condition that a normal orthogonal set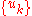
be closed is that the formal series for each function of a known closed normal orthogonal set 
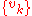in terms of 
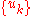converge in the mean to that function.
The theorem was proved by Giuseppe Lauricella
in 1912.
Orthogonal functions
In mathematics, two functions f and g are called orthogonal if their inner product \langle f,g\rangle is zero for f ≠ g. Whether or not two particular functions are orthogonal depends on how their inner product has been defined. A typical definition of an inner product for functions is...
, Lauricella's theorem provides a condition for checking the closure of a set of orthogonal functions, namely:
Theorem. A necessary and sufficient condition that a normal orthogonal set
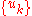be closed is that the formal series for each function of a known closed normal orthogonal set 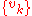in terms of 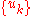converge in the mean to that function.The theorem was proved by Giuseppe Lauricella
Giuseppe Lauricella
Giuseppe Lauricella was an Italian mathematician who is remembered today for his contributions to analysis and the theory of elasticity....
in 1912.