
Lebesgue's density theorem
Encyclopedia
In mathematics
, Lebesgue's density theorem states that for any Lebesgue measurable set
A, the "density" of A is 1 at almost every point in A. Intuitively, this means that the "edge" of A, the set of points in A whose "neighborhood" is partially in A and partially outside of A, is negligible
.
Let μ be the Lebesgue measure on the Euclidean space
Rn and A be a Lebesgue measurable subset of Rn. Define the approximate density of A in a ε-neighborhood of a point x in Rn as
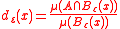
where Bε denotes the closed ball of radius ε centered at x.
Lebesgue's density theorem asserts that for almost every point x of A the density
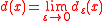
exists and is equal to 1.
In other words, for every measurable set A, the density of A is 0 or 1 almost everywhere
in Rn. However, it is a curious fact that if μ(A) > 0 and , then there are always points of Rn where the density is neither 0 nor 1.
For example, given a square in the plane, the density at every point inside the square is 1, on the edges is 1/2, and at the corners is 1/4. The set of points in the plane at which the density is neither 0 nor 1 is non-empty (the square boundary), but it is negligible.
The Lebesgue density theorem is a particular case of the Lebesgue differentiation theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Lebesgue's density theorem states that for any Lebesgue measurable set
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
A, the "density" of A is 1 at almost every point in A. Intuitively, this means that the "edge" of A, the set of points in A whose "neighborhood" is partially in A and partially outside of A, is negligible
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
.
Let μ be the Lebesgue measure on the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn and A be a Lebesgue measurable subset of Rn. Define the approximate density of A in a ε-neighborhood of a point x in Rn as
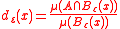
where Bε denotes the closed ball of radius ε centered at x.
Lebesgue's density theorem asserts that for almost every point x of A the density
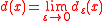
exists and is equal to 1.
In other words, for every measurable set A, the density of A is 0 or 1 almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
in Rn. However, it is a curious fact that if μ(A) > 0 and , then there are always points of Rn where the density is neither 0 nor 1.
For example, given a square in the plane, the density at every point inside the square is 1, on the edges is 1/2, and at the corners is 1/4. The set of points in the plane at which the density is neither 0 nor 1 is non-empty (the square boundary), but it is negligible.
The Lebesgue density theorem is a particular case of the Lebesgue differentiation theorem
Lebesgue differentiation theorem
In mathematics, the Lebesgue differentiation theorem is a theorem of real analysis, which states that for almost every point, the value of an integrable function is the limit of infinitesimal averages taken about the point...
.

