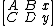Lehmer's GCD algorithm, named after Derrick Henry Lehmer

Derrick Henry Lehmer

Derrick Henry "Dick" Lehmer was an American mathematician who refined Édouard Lucas' work in the 1930s and devised the Lucas–Lehmer test for Mersenne primes...

, is a rather fast GCD

Greatest common divisor

In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...

 algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

, an improvement on the simpler but slower Euclidean algorithm

Euclidean algorithm

In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...

. It is mainly used for big integers that have a representation as a string of digits relative to some chosen numeral system base

Radix

In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...

, say β = 1000 or β = 2³².

Algorithm

Lehmer noted that most of the quotient

Quotient

In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...

s from each step of the division part of the standard algorithm are small. (For example, Knuth

Donald Knuth

Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...

 observed that the quotients 1, 2, and 3 comprise 67.7% of all quotients.) Those small quotients can be identified from only a few leading digits. Thus the algorithm starts by splitting off those leading digits and computing the sequence of quotients as long as it is correct.

Say we want to obtain the GCD of the two integers a and b. Let a ≥ b.

• If b contains only one digit (in the chosen base
  Radix
  In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
  
  , say β = 1000 or β = 2³²), use some other method, such as the Euclidean algorithm
  Euclidean algorithm
  In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
  
  , to obtain the result.
• If a and b differ in the length of digits, perform a division so that a and b are equal in length, with length equal to m.
• Outer loop: Iterate until one of a or b is zero:
  • Decrease m by one. Let x be the leading (most significant) digit in a, x = a div β ^m and y the leading digit in b, y = b div β ^m.
  • Initialize a 2 by 3 matrix
    Matrix (mathematics)
    In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
    
    

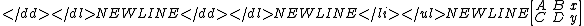  to an extended identity matrix

  Identity matrix

  In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...

  
  

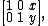
  • and perform the euclidean algorithm simultaneously on the pairs (x + A, y + C) and (x + B, y + D), until the quotients differ. That is, iterate as an inner loop:

    • Compute the quotients w₁ of the long divisions of (x + A) by (y + C) and w₂ of (x + B) by (y + D) respectively. Also let w be the (not computed) quotient from the current long division in the chain of long divisions of the euclidean algorithm.
      • If w₁ ≠ w₂, then break out of the inner iteration. Else set w to w₁ (or w₂).
      • Replace the current matrix

      

      with the matrix product

      

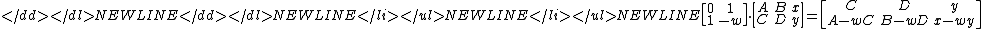
      • • according to the matrix formulation of the extended euclidean algorithm.

          • If B ≠ 0, go to the start of the inner loop.
        • If B = 0, we have reached a deadlock; perform a normal step of the euclidean algorithm with a and b, and restart the outer loop.
        • Set a to aA + bB and b to Ca + Db (again simultaneously). This applies the steps of the euclidean algorithm that were performed on the leading digits in compressed form to the long integers a and b. If b ≠ 0 go to the start of the outer loop.

      The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.