
Linear temporal logic to Büchi automaton
Encyclopedia
In formal verification
,
the model checking
method needs to obtain a Büchi automaton
(BA) from a Linear temporal logic
(LTL) formula.
There are algorithms that translates a LTL formula to an equivalent BA
, i.e., the LTL formula and the BA recognizes the same ω-language.
This transformation is normally done in two steps.
The first step produces a generalized Büchi automaton
(GBA) from a LTL formula.
The second step translates this GBA into a BA, which involves relatively
easy construction.
Since LTL is strictly less expressive than BA, the reverse construction is not possible.
There are multiple algorithm for transforming LTL to GBA.
These algorithms differ in their construction strategies but they
all have common underlying principle, i.e.,
each state in the constructed automaton represents a set of LTL formulas
that are expected to be satisfied by the remaining input word after occurrence of the state during a run.
For each LTL formula f' without ¬ as top symbol, let neg(f') = ¬f', neg(¬f') = f'.
For a special case f'=true, let neg(true) = false.
For a LTL formula f, Let cl( f ) be a smallest set of formulas that satisfies the following conditions:
cl( f ) is closure of sub-formulas of f under negation.
Note that cl( f ) may contain formulas that are not in negation normal form.
The subsets of cl( f ) are going to serve as states of the equivalent GBA.
We want that a state labelled by a subset M ⊂ cl( f ) will accept a word iff it satisfies every formula in M and violates every formula in cl( f )/M.
For this reason,
we will exclude each formula subset M that is clearly inconsistent
or subsumed by a strictly super set M' such that M and M' are equiv-satisfiable.
A set M ⊂ cl( f ) is consistent if it satisfies the following conditions:
Let cs( f ) be set of consistent subsets of cl( f ).
We are going to use only cs( f ) as the states of GBA.
An equivalent GBA
to f is A= ({init}∪cs( f ), 2AP, Δ,{init},F), where
The three conditions in definition of Δ1 ensure that any run of A does not violate semantics of the temporal operators.
Note that F is a set of sets.
The sets in F are defined to capture a property of operator U that can not be verified by comparing two consecutive states in a run, i.e.,
if f1 U f2 is true in some state then eventually f2 is true at some state later.
Proof of correctness of the above construction
Let ω-word w= a1, a2,... over alphabet 2AP. Let wi = ai, ai+1,... .
Let Mw = { f' ∈ cl(f) | w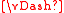 f' }, which we call satisfying set.
f' }, which we call satisfying set.
Due to the definition of cs(f), Mw ∈ cs(f).
We can define a sequence
ρw = init, Mw1, Mw2,... .
Due to the definition of A,
if w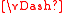 f then ρw must be an accepting run of A over w.
f then ρw must be an accepting run of A over w.
Conversely, lets assume A accepts w.
Let ρ = init, M1, M2,... be a run of A over w.
The following theorem completes the rest of the correctness proof.
Theorem 1: For all i > 0, Mwi = Mi.
Proof: The proof is by induction on the structure of f' ∈ cl(f).
Due to the above theorem, Mw1 = M1. Due to the definition of the transitions of A, f ∈ M1. Therefore, f ∈ Mw1 and w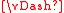 f.
f.
, and Wolper.
The above construction creates exponentially many states upfront and many of those states may be unreachable.
The following algorithm has two steps.
In step one, it incrementally constructs a directed graph stored in a tableaux.In step two, it builds an labeled generalized Büchi automaton(LGBA) by defining nodes of the graph as states and directed edges as transitions.
This algorithm takes reachability into account and may produce a smaller automaton but the worst case complexity remains the same.
The nodes of the graph are labeled by sets of formulas and are obtained by decomposing formulas according to their Boolean structure, and by expanding the temporal operators in order to separate what has to be true immediately from what has to be true from the next state on. For example, let us assume that an LTL formula f1 U f2 appears in the label of a node.
f1 U f2 is equivalent to f2 ∨ ( f1 ∧ X(f1 U f2) ).
The equivalent expansion suggests that f1 U f2 is true in one of the following two conditions.
We can encode this logic by creating two states(nodes) of the automaton and the automaton may non-deterministically jump to either of them.
In the first case, we have offloaded a part of burden of proof in the next time step
therefore we also create another state(node) that will carry the obligation for next time step in its label.
We also need to consider temporal operator R that may cause such case split.
f1 R f2 is equivalent to ( f1 ∧ f2) ∨ ( f2 ∧ X(f1 R f2) )
and this equivalent expansion suggests that f1 R f2 is true in one of the following two conditions.
To avoid many cases in the following algorithm, let us define functions new1, next1 and new2 that encode the above equivalences in the following table.
We have also added disjunction case in the above table since it also cause a case split in the automaton.
Following are the two steps of the algorithm.
Step 1. create_graph
In the following box, we present the first part of the algorithm that builds a directed graph. create_graph is the entry function, which expects the input formula f in the negation normal form. It calls recursive function expand that builds the graph by populating global variables Nodes, Incoming, Now, and Next.
The set Nodes stores the set of nodes in the graph. The map Incoming maps each node of Nodes to a subset of Nodes ∪ {init}, which defines the set of incoming edges.
Incoming of a node may also contain a special symbol init that is used in the final automaton construction to decide the set of initial states.
Now and Next map each node of Nodes to a set of LTL formulas.
For a node q, Now(q) denotes the set of formulas that must be satisfied by the rest of the input word if the automaton is currently at node(state) q.
Next(q) denotes the set of of formulas that must be satisfied by the rest of the input word if the automaton is currently at the next node(state) after q.
typedefs
LTL: LTL formulas
LTLSet: Sets of LTL formulas
NodeSet: Sets of graph nodes ∪ {init}
globals
Nodes : set of graph nodes := ∅
Incoming: Nodes → NodeSet := ∅
Now : Nodes → LTLSet := ∅
Next : Nodes → LTLSet := ∅
function create_graph(LTL f){
expand({f}, ∅, ∅, {init} )
return (Nodes, Now, Incoming)
}
function expand(LTLSet new, LTLSet old, LTLSet next, NodeSet incoming){
1: if new = ∅ then
2: if ∃q ∈ Nodes: Next(q)=next ∧ Now(q)=old then
3: Incoming(q) := Incoming(q) ∪ incoming
4: else
5: q := new_node
6: Nodes := Nodes ∪ {q}
7: Incoming(q) := incoming
8: Now(q) := old
9: Next(q) := next
10: expand(Next(q), ∅, ∅, {q})
11: else
12: f ∈ new
13: new := new\{f}
14: old := old ∪ {f}
15: match f with
16: | true, false, p, or ¬p, where p ∈ AP →
17: if f = false ∨ neg(f) ∈ old then
18: skip
19: else
20: expand(new, old, next, incoming)
21: | f1 ∧ f2 →
22: expand(new ∪ {f1,f2}, old, next, incoming)
23: | X g →
24: expand(new, old, next ∪ {g}, incoming)
25: | f1 ∨ f2, f1 U f2, or f1 R f2 →
26: expand(new ∪ (new1(f)/old), old, next ∪ next1(f), incoming)
27: expand(new ∪ (new2(f)/old), old, next, incoming)
28: return
}
The code of expand is labelled with line numbers for easy reference.
Each call to expand aims to add a node and its successors nodes in the graph.
The parameters of the call describes a potential new node.
The first parameter new contains the set of formulas that are yet to be expanded. The second parameter old contains the set of formulas that are already expanded.
The third parameter next is the set of the formula using which successor node will be created.
The fourth parameter incoming defines set of incoming edges when the node is added to the graph.
At line 1, the if condition checks if new contains any formula to be expanded.
If the new is empty then at line 2 the if condition checks if there already exists a state q' with same set of expanded formulas.
If that is the case then then we do not add a redundant node, but we add parameter incoming in Incoming(q') at line 3.
Otherwise, we add a new node q using the parameters at lines 5--9
and we start expanding a successor node of q using next(q) as its unexpanded
set of formulas at line 10.
In the case new is not empty then we have more formulas to expand and
control jumps from line 1 to 12.
At lines 12--14, a formula f from new is selected and moved to old.
Depending on structure of f, rest of the function executes.
If f is a literal then expansion continues at line 20, but if old already contains
neg(f) or f=false then old contains an inconsistent formula and we discard this node by not making any recursive all at line 18.
If f = f1 ∧ f2 then f1 and f2 are added to new and a recursive call is made for further expansion at line 22.
If f = X f1 then f1 is added to next for the successor of the current node under consideration at line 24.
If f = f1 ∨ f2, f = f1 U f2, or f = f1 R f2 then the current node is divided into two nodes
and for each node a recursive call is made. For the recursive calls, new and next are modified using functions new1, next1, and new2 that were defined in the above table.
Step 2. LGBA construction
Let (Nodes, Now, Incoming) = create_graph(f).
An equivalent LGBA to f is A=(Nodes, 2AP, L, Δ, Q0, F), where
Note that node labels in the algorithmic construction does not not contain negation of sub-formulas of f. In the declarative construction a node has the set of formulas that are expected to be true. The algorithmic construction ensures the correctness without the need of all the true formulas to be present in a node label.
Formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal methods of mathematics .- Usage :Formal verification can be...
,
the model checking
Model checking
In computer science, model checking refers to the following problem:Given a model of a system, test automatically whether this model meets a given specification....
method needs to obtain a Büchi automaton
Büchi automaton
In computer science and automata theory, a Büchi automaton is a type of ω-automaton, which extends a finite automaton to infinite inputs. It accepts an infinite input sequence iff there exists a run of the automaton that visits one of the final states infinitely often. Büchi automata recognize the...
(BA) from a Linear temporal logic
Linear temporal logic
In logic, Linear temporal logic is a modal temporal logic with modalities referring to time. In LTL, one can encode formulae about the future of paths such as that a condition will eventually be true, that a condition will be true until another fact becomes true, etc. It is a fragment of the more...
(LTL) formula.
There are algorithms that translates a LTL formula to an equivalent BA
, i.e., the LTL formula and the BA recognizes the same ω-language.
This transformation is normally done in two steps.
The first step produces a generalized Büchi automaton
Generalized Büchi automaton
In automata theory, generalized Büchi automaton is a variant of Büchi automaton. The difference with the Büchi automaton is its accepting condition, i.e., a set of sets of states. A run is accepted by the automaton if it visits at least one state of every set of the accepting condition infinitely...
(GBA) from a LTL formula.
The second step translates this GBA into a BA, which involves relatively
easy construction.
Since LTL is strictly less expressive than BA, the reverse construction is not possible.
There are multiple algorithm for transforming LTL to GBA.
These algorithms differ in their construction strategies but they
all have common underlying principle, i.e.,
each state in the constructed automaton represents a set of LTL formulas
that are expected to be satisfied by the remaining input word after occurrence of the state during a run.
Transformation from LTL to GBA
Here two algorithms are presented for the construction. The first one provides a declarative and easy to understand construction. The second one provides an algorithmic and efficient construction. Both the algorithms assume that the input formula f is constructed using the set of propositional variables AP and f is in negation normal form.For each LTL formula f' without ¬ as top symbol, let neg(f') = ¬f', neg(¬f') = f'.
For a special case f'=true, let neg(true) = false.
Declarative construction
Before describing the construction, we need to present a few auxiliary definitions.For a LTL formula f, Let cl( f ) be a smallest set of formulas that satisfies the following conditions:
|
|
cl( f ) is closure of sub-formulas of f under negation.
Note that cl( f ) may contain formulas that are not in negation normal form.
The subsets of cl( f ) are going to serve as states of the equivalent GBA.
We want that a state labelled by a subset M ⊂ cl( f ) will accept a word iff it satisfies every formula in M and violates every formula in cl( f )/M.
For this reason,
we will exclude each formula subset M that is clearly inconsistent
or subsumed by a strictly super set M' such that M and M' are equiv-satisfiable.
A set M ⊂ cl( f ) is consistent if it satisfies the following conditions:
|
|
Let cs( f ) be set of consistent subsets of cl( f ).
We are going to use only cs( f ) as the states of GBA.
An equivalent GBA
Generalized Büchi automaton
In automata theory, generalized Büchi automaton is a variant of Büchi automaton. The difference with the Büchi automaton is its accepting condition, i.e., a set of sets of states. A run is accepted by the automaton if it visits at least one state of every set of the accepting condition infinitely...
to f is A= ({init}∪cs( f ), 2AP, Δ,{init},F), where
- Δ = Δ1 ∪ Δ2
- (M, a, M') ∈ Δ1 iff ( M' ∩AP ) ⊆ a ⊆ {p ∈ AP | ¬p ∉ M' } and:
- X f1 ∈ M iff f1 ∈ M';
- f1 U f2 ∈ M iff f2 ∈ M or ( f1 ∈ M and f1 U f2 ∈ M' );
- f1 R f2 ∈ M iff f1 ∧ f2 ∈ M or ( f2 ∈ M and f1 R f2 ∈ M' )
- Δ2 = { (init, a, M') | ( M' ∩AP ) ⊆ a ⊆ {p ∈ AP | ¬p ∉ M' } and f ∈ M' }
- (M, a, M') ∈ Δ1 iff ( M' ∩AP ) ⊆ a ⊆ {p ∈ AP | ¬p ∉ M' } and:
- For each f1 U f2 ∈ cl( f ), {M ∈ cs( f ) | f2 ∈ M or ¬(f1 U f2) ∈ M } ∈ F
The three conditions in definition of Δ1 ensure that any run of A does not violate semantics of the temporal operators.
Note that F is a set of sets.
The sets in F are defined to capture a property of operator U that can not be verified by comparing two consecutive states in a run, i.e.,
if f1 U f2 is true in some state then eventually f2 is true at some state later.
Proof of correctness of the above construction
Let ω-word w= a1, a2,... over alphabet 2AP. Let wi = ai, ai+1,... .
Let Mw = { f' ∈ cl(f) | w
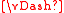 f' }, which we call satisfying set.
f' }, which we call satisfying set.Due to the definition of cs(f), Mw ∈ cs(f).
We can define a sequence
ρw = init, Mw1, Mw2,... .
Due to the definition of A,
if w
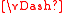 f then ρw must be an accepting run of A over w.
f then ρw must be an accepting run of A over w.Conversely, lets assume A accepts w.
Let ρ = init, M1, M2,... be a run of A over w.
The following theorem completes the rest of the correctness proof.
Theorem 1: For all i > 0, Mwi = Mi.
Proof: The proof is by induction on the structure of f' ∈ cl(f).
- Base cases:
- f' = true. By definitions, f' ∈ Mwi and f' ∈ Mi.
- f' = p. By definition of A, p ∈ Mi iff p ∈ ai iff p ∈ Mwi.
- Induction steps:
- f' = f1 ∧ f2. Due to the definition of consistent sets, f1 ∧ f2 ∈ Mi iff f1 ∈ Mi and f2 ∈ Mi. Due to induction hypothesis, f1 ∈ Mwi and f2 ∈ Mwi. Due to definition of satisfying set, f1 ∧ f2 ∈ Mwi.
- f' = ¬f1, f' = f1 ∨ f2, f' = X f1 or f' = f1 R f2. The proofs are very similar to the last one.
- f' = f1 U f2. The proof of equality is divided in two entailment proofs.
- If f1 U f2 ∈ Mi, then f1 U f2 ∈ Mwi. By the definition of the transitions of A, we can have the following two cases.
- f2 ∈ Mi. By induction hypothesis, f2 ∈ Mwi. So, f1 U f2 ∈ Mwi.
- f1 ∈ Mi and f1 U f2 ∈ Mi+1. And due to the acceptance condition of A, there is at least one index j ≥ i such that f2 ∈ Mj. Let j' be the smallest of these indices. We prove the result by induction on k = {j',j'-1,...,i+1,i}. If k = j', then f2 ∈ Mk, we apply same argument as in the case of f2 ∈ Mi. If i ≤ k < j', then f2 ∉ Mk, and so f1 ∈ Mk and f1 U f2 ∈ Mk+1. Due to induction hypothesis on f', we have f1 ∈ Mwk. Due to induction hypothesis on indices, we also have f1 U f2 ∈ Mwk+1. Due to definition of the semantics of LTL, f1 U f2 ∈ Mwk.
- If f1 U f2 ∈ Mwi, then f1 U f2 ∈ Mi. Due to the LTL semantics, we can have the following two cases.
- f2 ∈ Mwi. By induction hypothesis, f2 ∈ Mi. So, f1 U f2 ∈ Mi.
- f1 ∈ Mwi and f1 U f2 ∈ Mwi+1. Due to the LTL semantics, there is at least one index j ≥ i such that f2 ∈ Mj. Let j' be the smallest of these indices. Proceed now as in proof of the converse entailment.
- If f1 U f2 ∈ Mi, then f1 U f2 ∈ Mwi. By the definition of the transitions of A, we can have the following two cases.
Due to the above theorem, Mw1 = M1. Due to the definition of the transitions of A, f ∈ M1. Therefore, f ∈ Mw1 and w
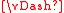 f.
f.Gerth et al. algorithm
The following algorithm is due to Gerth, Peled, VardiMoshe Y. Vardi
Moshe Ya'akov Vardi is a Professor of Computer Science at Rice University, USA. He is the Karen Ostrum George Professor in Computational Engineering, Distinguished Service Professor, and Director of the Computer and Information Technology Institute...
, and Wolper.
The above construction creates exponentially many states upfront and many of those states may be unreachable.
The following algorithm has two steps.
In step one, it incrementally constructs a directed graph stored in a tableaux.In step two, it builds an labeled generalized Büchi automaton(LGBA) by defining nodes of the graph as states and directed edges as transitions.
This algorithm takes reachability into account and may produce a smaller automaton but the worst case complexity remains the same.
The nodes of the graph are labeled by sets of formulas and are obtained by decomposing formulas according to their Boolean structure, and by expanding the temporal operators in order to separate what has to be true immediately from what has to be true from the next state on. For example, let us assume that an LTL formula f1 U f2 appears in the label of a node.
f1 U f2 is equivalent to f2 ∨ ( f1 ∧ X(f1 U f2) ).
The equivalent expansion suggests that f1 U f2 is true in one of the following two conditions.
- f1 holds in the current time and (f1 U f2) holds in the next time step, or
- f2 holds in the current time step
We can encode this logic by creating two states(nodes) of the automaton and the automaton may non-deterministically jump to either of them.
In the first case, we have offloaded a part of burden of proof in the next time step
therefore we also create another state(node) that will carry the obligation for next time step in its label.
We also need to consider temporal operator R that may cause such case split.
f1 R f2 is equivalent to ( f1 ∧ f2) ∨ ( f2 ∧ X(f1 R f2) )
and this equivalent expansion suggests that f1 R f2 is true in one of the following two conditions.
- f2 holds in the current time and (f1 R f2) holds in the next time step, or
- ( f1 ∧ f2) holds in the current time step.
To avoid many cases in the following algorithm, let us define functions new1, next1 and new2 that encode the above equivalences in the following table.
| f | new1(f) | next1(f) | new2(f) |
|---|---|---|---|
| f1 U f2 | {f1} | { f1 U f2 } | {f2} |
| f1 R f2 | {f2} | { f1 R f2 } | {f1,f2} |
| f1 ∨ f2 | {f2} | ∅ | {f1} |
We have also added disjunction case in the above table since it also cause a case split in the automaton.
Following are the two steps of the algorithm.
Step 1. create_graph
In the following box, we present the first part of the algorithm that builds a directed graph. create_graph is the entry function, which expects the input formula f in the negation normal form. It calls recursive function expand that builds the graph by populating global variables Nodes, Incoming, Now, and Next.
The set Nodes stores the set of nodes in the graph. The map Incoming maps each node of Nodes to a subset of Nodes ∪ {init}, which defines the set of incoming edges.
Incoming of a node may also contain a special symbol init that is used in the final automaton construction to decide the set of initial states.
Now and Next map each node of Nodes to a set of LTL formulas.
For a node q, Now(q) denotes the set of formulas that must be satisfied by the rest of the input word if the automaton is currently at node(state) q.
Next(q) denotes the set of of formulas that must be satisfied by the rest of the input word if the automaton is currently at the next node(state) after q.
typedefs
LTL: LTL formulas
LTLSet: Sets of LTL formulas
NodeSet: Sets of graph nodes ∪ {init}
globals
Nodes : set of graph nodes := ∅
Incoming: Nodes → NodeSet := ∅
Now : Nodes → LTLSet := ∅
Next : Nodes → LTLSet := ∅
function create_graph(LTL f){
expand({f}, ∅, ∅, {init} )
return (Nodes, Now, Incoming)
}
function expand(LTLSet new, LTLSet old, LTLSet next, NodeSet incoming){
1: if new = ∅ then
2: if ∃q ∈ Nodes: Next(q)=next ∧ Now(q)=old then
3: Incoming(q) := Incoming(q) ∪ incoming
4: else
5: q := new_node
6: Nodes := Nodes ∪ {q}
7: Incoming(q) := incoming
8: Now(q) := old
9: Next(q) := next
10: expand(Next(q), ∅, ∅, {q})
11: else
12: f ∈ new
13: new := new\{f}
14: old := old ∪ {f}
15: match f with
16: | true, false, p, or ¬p, where p ∈ AP →
17: if f = false ∨ neg(f) ∈ old then
18: skip
19: else
20: expand(new, old, next, incoming)
21: | f1 ∧ f2 →
22: expand(new ∪ {f1,f2}, old, next, incoming)
23: | X g →
24: expand(new, old, next ∪ {g}, incoming)
25: | f1 ∨ f2, f1 U f2, or f1 R f2 →
26: expand(new ∪ (new1(f)/old), old, next ∪ next1(f), incoming)
27: expand(new ∪ (new2(f)/old), old, next, incoming)
28: return
}
The code of expand is labelled with line numbers for easy reference.
Each call to expand aims to add a node and its successors nodes in the graph.
The parameters of the call describes a potential new node.
The first parameter new contains the set of formulas that are yet to be expanded. The second parameter old contains the set of formulas that are already expanded.
The third parameter next is the set of the formula using which successor node will be created.
The fourth parameter incoming defines set of incoming edges when the node is added to the graph.
At line 1, the if condition checks if new contains any formula to be expanded.
If the new is empty then at line 2 the if condition checks if there already exists a state q' with same set of expanded formulas.
If that is the case then then we do not add a redundant node, but we add parameter incoming in Incoming(q') at line 3.
Otherwise, we add a new node q using the parameters at lines 5--9
and we start expanding a successor node of q using next(q) as its unexpanded
set of formulas at line 10.
In the case new is not empty then we have more formulas to expand and
control jumps from line 1 to 12.
At lines 12--14, a formula f from new is selected and moved to old.
Depending on structure of f, rest of the function executes.
If f is a literal then expansion continues at line 20, but if old already contains
neg(f) or f=false then old contains an inconsistent formula and we discard this node by not making any recursive all at line 18.
If f = f1 ∧ f2 then f1 and f2 are added to new and a recursive call is made for further expansion at line 22.
If f = X f1 then f1 is added to next for the successor of the current node under consideration at line 24.
If f = f1 ∨ f2, f = f1 U f2, or f = f1 R f2 then the current node is divided into two nodes
and for each node a recursive call is made. For the recursive calls, new and next are modified using functions new1, next1, and new2 that were defined in the above table.
Step 2. LGBA construction
Let (Nodes, Now, Incoming) = create_graph(f).
An equivalent LGBA to f is A=(Nodes, 2AP, L, Δ, Q0, F), where
- L = { (q,a) | q ∈ Nodes and (Now(q) ∩ AP) ⊆ a ⊆ {p ∈ P | ¬p ∉ Now(q) } }
- Δ = {(q,q')| q,q' ∈ Nodes and q ∈ Incoming(q') }
- Q0 = { q ∈ Nodes | init ∈ Now(q) }
- F = { { q ∈ Nodes | f2 ∈ Now(q) or (f1 U f2) ∉ Now(q) } | f1 U f2 ∈ cl( f ) }
Note that node labels in the algorithmic construction does not not contain negation of sub-formulas of f. In the declarative construction a node has the set of formulas that are expected to be true. The algorithmic construction ensures the correctness without the need of all the true formulas to be present in a node label.

