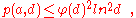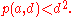Linnik's theorem in analytic number theory

Analytic number theory

In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...

 answers a natural question after Dirichlet's theorem on arithmetic progressions

Dirichlet's theorem on arithmetic progressions

In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...

. It asserts that, if we denote p(a,d) the least prime in the arithmetic progression

Primes in arithmetic progression

In number theory, the phrase primes in arithmetic progression refers to at least three prime numbers that are consecutive terms in an arithmetic progression, for example the primes ....

where n runs through the positive integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s and a and d are any given positive coprime

Coprime

In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...

 integers with 1 ≤ a ≤ d - 1, then there exist positive c and L such that:

The theorem is named after Yuri Vladimirovich Linnik, who proved it in 1944. Although Linnik's proof showed c and L to be effectively computable

Effective results in number theory

For historical reasons and in order to have application to the solution of Diophantine equations, results in number theory have been scrutinised more than in other branches of mathematics to see if their content is effectively computable...

, he provided no numerical values for them.

The constant L is called Linnik's constant and the following table shows the progress that has been made on determining its size.

L ≤	Year of publication	Author
10000	1957	Pan Pan Chengdong Pan Chengdong was a Chinese mathematician made contributions in number theory, including the Goldbach's conjecture...
5448	1958	Pan
777	1965	Chen Chen Jingrun Chen Jingrun was a Chinese mathematician who made significant contributions to number theory.- Personal life :Chen was the third son in a large family from Fuzhou, Fujian, China. His father was a postal worker. Chen Jingrun graduated from the Mathematics Department of Xiamen University in 1953...
630	1971	Jutila Matti Jutila Matti Jutila is a mathematician and professor at the University of Turku. He researches in the field of analytic number theory.He repeatedly succeeded in lowering the upper bound for Linnik's constant.-External links:...
550	1970	Jutila
168	1977	Chen
80	1977	Jutila
36	1977	Graham Sidney Graham Sidney West Graham is a mathematician interested in analytic number theory and professor at Central Michigan University. His received his Ph.D., which was supervised by Hugh Montgomery, from the University of Michigan in 1977. In his Ph.D. thesis he lowered the upper bound for Linnik's constant to...
20	1981	Graham (submitted before Chen's 1979 paper)
17	1979	Chen
16	1986	Wang
13.5	1989	Chen and Liu
8	1990	Wang
5.5	1992	Heath-Brown Roger Heath-Brown David Rodney "Roger" Heath-Brown F.R.S. , is a British mathematician working in the field of analytic number theory. He was an undergraduate and graduate student of Trinity College, Cambridge; his research supervisor was Alan Baker...
5.2	2009	Xylouris

Moreover, in Heath-Brown's result the constant c is effectively computable.

It is known that L ≤ 2 for almost all

Almost all

In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....

 integers d.

On the generalized Riemann hypothesis

Generalized Riemann hypothesis

The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...

 it can be shown that

where is the totient function.

It is also conjectured that: