
Lévy flight foraging hypothesis
Encyclopedia
The Lévy flight foraging hypothesis is a hypothesis
in the field of biology
that may be stated as follows:
. This similarity led to interest in trying to understand how animals move via the analogy to Brownian motion. This conventional wisdom held until the early 1990s. However, starting in the late 1980s, evidence began to accumulate that did not fit the theoretical predictions.
In 1999, a theoretical investigation of the properties of Lévy flight
s showed that an inverse square distribution of flight times or distances could optimize the search efficiency under certain circumstances. Specifically, a search based on a Lévy walk, consisting of a constant velocity search following a Lévy flight path, is optimal for searching sparsely and randomly distributed revisitable targets.
The most extensive empirical studies to test the Lévy flight foraging hypothesis were undertaken by Sims et al. and by Humphries et al.. These extensive studies, involving more than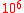 data points each, have lent a new level of credibility to the hypothesis.
data points each, have lent a new level of credibility to the hypothesis.
Hypothesis
A hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
in the field of biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
that may be stated as follows:
Since Lévy flights and walks can optimize search efficiencies, therefore natural selection should have led to adaptations for Lévy flight foraging.
Background
The movement of animals closely resembles in many ways the random walks of dust particles in a fluidBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
. This similarity led to interest in trying to understand how animals move via the analogy to Brownian motion. This conventional wisdom held until the early 1990s. However, starting in the late 1980s, evidence began to accumulate that did not fit the theoretical predictions.
In 1999, a theoretical investigation of the properties of Lévy flight
Lévy flight
A Lévy flight is a random walk in which the step-lengths have a probability distribution that is heavy-tailed. When defined as a walk in a space of dimension greater than one, the steps made are in isotropic random directions...
s showed that an inverse square distribution of flight times or distances could optimize the search efficiency under certain circumstances. Specifically, a search based on a Lévy walk, consisting of a constant velocity search following a Lévy flight path, is optimal for searching sparsely and randomly distributed revisitable targets.
The most extensive empirical studies to test the Lévy flight foraging hypothesis were undertaken by Sims et al. and by Humphries et al.. These extensive studies, involving more than
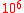 data points each, have lent a new level of credibility to the hypothesis.
data points each, have lent a new level of credibility to the hypothesis.

